A integral está relacionada ao problema do calculo de área sobre curvas, volumes e muitas outras apllicações.

Introdução a Integral

As integrais podem ser vistas como antiderivadas, ou seja, a operação inversa da derivada. Vamos agora ver isso no Maxima, peguemos os casos do exercício feito na aula anterior:

1. $$ f(x) = exp(x) + x^7$$
2. $$ f(x) = x + sin(x) $$
3. $$ f(x) = 5x^3 + 2$$
4. $$ f(x) = cos(x) + sin(x) $$
5. $$ f(x) = x^2 + x^3cos(x)$$
6. $$ f(x) = exp(x) ln(x) $$
7. $$ f(x) = x^5sin(x)$$
8. $$ f(x) = 1/x $$
9. $$ f(x) = 1/x^2 $$
10. $$ f(x) = exp(x)/x $$
11. $$ f(x) = sin(x)/x^2$$

<box green 80% | Integral no Máxima> A função do máxima que opera integrais é integrate que tem como argumentos principais a função e a variável a ser integrada. Há duas formas da função no Máxima,

integrate(2*x, x);
'integrate(2*x,x);

A primeira retorna a solução da Integral, a segunda, a representação simbólica da Integral. </box>

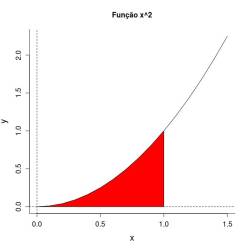Podemos pensar a integral definida como a área resultante sob a curva da função em um dado intervalo. Vamos visualizar isso graficamente com a nossa já conhecida função quadratica $f(x)=x^2$ a área no intervalo de 0 até 1.

$\int_0^1 f(x)~dx$

##############################
## área sob a curva f(x)= x^2;
## no intervalo 0 a 1
#############################

seq.x=seq(0,1.5, by=0.1)
seq.y=seq.x^2
plot(seq.x,seq.y, type="l", bty="l", cex.lab=1.5, cex.axis=1.2, main= "Função x^2", xlab="x", ylab="y")
#plot(seq.x,seq.y, type="l")
abline(v=0, lty=2)
abline(h=0, lty=2)
seq.x1=seq(0,1,by=0.1)
seq.y1=seq.x1^2
polygon(c(1,0,seq.x1,1), c(0,0,seq.y1,0),col="red")
#savePlot("area_x2.jpeg", type="jpeg")

###############################
#### Calculo dos retângulos ###
###############################
x11()
n.seq=length(seq.x1)
plot(seq.x,seq.y, type="l", bty="l", cex.lab=1.5, cex.axis=1.2, main= "Função x^2", xlab="x", ylab="y")
abline(v=0, lty=2)
abline(h=0, lty=2)
abline(v=1, lty=2)
barplot(height=seq.y1[-n.seq],width=0.1, space=0, col="red", add=TRUE)
x11()
n.seq=length(seq.x1)
plot(seq.x,seq.y, type="l", bty="l", cex.lab=1.5, cex.axis=1.2, main= "Função x^2", xlab="x", ylab="y")
abline(v=0, lty=2)
abline(h=0, lty=2)
abline(v=1, lty=2)
barplot(height=seq.y1[-n.seq],width=0.1, space=0, col="red", add=TRUE)