VIII) MODELOS MATRICIAIS DE DINÂMICA DE POPULAÇÕES ESTRUTURADAS
Exercício 1
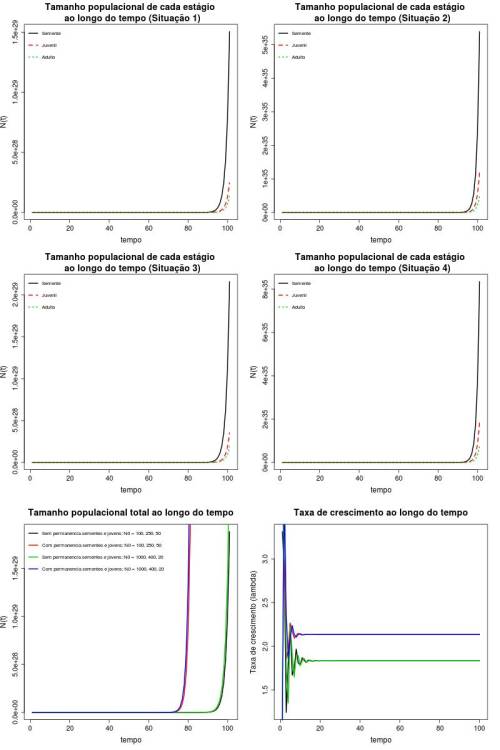
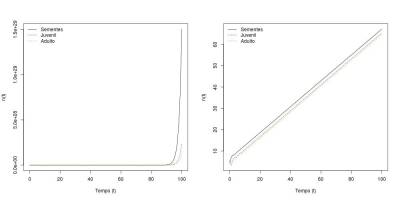
A projeção observada no gráfico é condizente com o esperado pelo modelo de crescimento populacional estruturado. Neste modelo as populações projetadas exibem crescimento exponencial, seja considerando o número total de indivíduos, seja considerando cada estágio etário separadamente. Percebe-se também, como esperado, que há uma fase de transiente antes de se chegar na fase exponencial do crescimento. Isso se deve o fato de ser necessário um tempo até que a taxa de crescimento (total ou de cada estágio) atinja um valor estável.
O padrão observado no gráfico b) é uma simples consequência de se logaritmar o número de indivíduos de cada estágio. Observando o logaritmo do número de indivíduos lineariza a função, como pode ser observado considerando a equação de crescimento exponencial. Isso fica mais claro observando a equação de crescimento contínuo, porém nosso modelo é discreto. No entanto, é razoável esperar que o crescimento discreto se comporta como uma aproximação do crescimento contínuo. Vejamos:
$ N_t = N_0e^{rt}$
$ log(N_t) = log(N_0e^{rt})$
$$ log(N_t) = log(N_0) + rt$$ O que torna a função linear, sendo $log(N_0)$ o intercepto e $r$ a inclinação. Em geral, esses gráficos estão informando que a cada passagem de uma unidade de tempo discreto uma mesma proporção ($r$) da população no tempo anterior é adicionada à população atual.
Exercício 2
A taxa de crescimento apresenta oscilações amortecidas até atingir um valor estável (fase de transiente), ao qual permanecerá indefinidamente na ausência de perturbações, determinando a fase de crescimento exponencial propriamente dito da população.
A taxa de crescimento tende a atingir um valor estável independentemente das condições iniciais ou dos valores dos parâmetros do modelo. Isso implica que em um modelo de dinâmica de populações estruturadas em que as taxas ou probabilidades de transição de cada estágio são constantes ao longo do tempo, as populações (e seus estágios) tendem inevitavelmente a um crescimento exponencial. Contudo, o que percebemos é que o valor em que a taxa de crescimento estabiliza depende dos valores dos parâmetros do modelo. Por outro lado, observa-se que alterando-se as condições iniciais, há um deslocamento da curva pois estamos alterando seu intercepto (quanto maior o número de indivíduos iniciais, mais para a esquerda a curva se desloca). Isso indica que, para um mesmo instante no tempo, uma população com mais indivíduos iniciais encontrará-se num ponto mais ou menos avançado da curva exponencial que será dada por uma taxa de crescimento igual para as duas populações comparadas.
Exercício 3
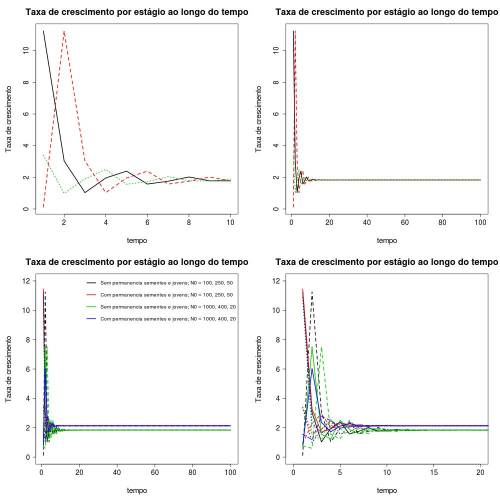
As contribuição de cada classe a cada tempo, para um tempo total de simulação = 10, estão disponíveis no arquivo a seguir. Este tempo total é muito pequeno, e o sistema ainda encontra-se saindo do transiente. Como será mostrado adiante, após um tempo suficiente para a estabilização das taxas de crescimento de cada estágio, a proporção de indivíduos em cada classe será constante e igual a:
Sementes: $0.042$ ou $4,2 \%$
Juvenis: $0.273$ ou $27,3 \%$
Adultos: $0.685$ ou $68,5 \%$
Proporções.txt (abrir no R)
O interessante é que se observa que a taxa de crescimento para cada estágio estabiliza num mesmo valor, que é igual ao valor que a taxa de crescimento da população como um todo estabiliza; nesta caso, $\lambda = 1,83$.
Exercício 4
A sobrevivência do adulto tem uma certa influência no destino da população, mas esta influencia não é muito contundente, pois as populações sempre crescem independente do nível de perturbação aplicado. O efeito de uma perturbação na sobrevivência do adulto para o nosso caso (as condições dadas pela nossa matriz de Leslie) será de reduzir um pouco a taxa de crescimento da população como um todo. A taxa de crescimento da população parece variar linearmente com o nível de perturbação (ou quanto menor for a sobrevivência dos adultos). No entanto, por mais severa que seja a perturbação nos adultos, a população estudada sempre crescerá pois suas taxas de crescimento no equilíbrio são sempre maiores que 1.
Sabendo-se que a sobrevivência dos adultos não afeta qualitativamente o destino da população, pode-se recomendar que a extração de palmitos seja feita coletando-se palmitos apenas das plantas adultas. O que se percebe é que um estoque de plantas adultas sempre existirá em qualquer tempo analisado. Por mais que todas as plantas adultas sejam retiradas da população pela extração do palmito num determinado tempo, novos indivíduos adultos aparecerão na população no tempo seguinte, dada a transição de alguns jovens para adultos durante este intervalo de tempo. Isso será válido se nossa matriz de Leslie possuir uma taxa ou probabilidade não nula de transição de jovens para adultos. Então, outra recomendação é que se evite extrair o palmito das plantas jovens, a fim de se ter um bom estoque de plantas adultas a cada passagem de tempo.
Como se observa, a transição de sementes para juvenis é mais importante para a sobrevivência da população. Embora o crescimento populacional se mantenha positivo para a maioria das condições de perturbação, quando a transição de sementes para juvenis é zerada, a taxa de crescimento populacional estabiliza em valores menores que 0, o que implica que a população entra em declinio, tendendo à extinção com o passar do tempo (este é o outro resultado possível de um modelo exponencial quando as taxas de crescimento (lambda) estão entre 0 e 1).
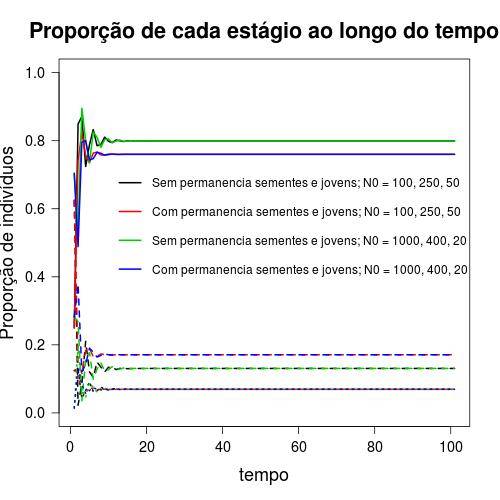
Dependendo do tipo de perturbação (qual taxa é perturbada), o nível de perturbação altera consideravelmente a a proporção de cada classe na população. Perturbações na sobrevivência dos adultos afetam muito pouco a proporção de cada classe, que permanece praticamente constante conforme varia o nível de perturbação. Já se a perturbação ocorre na transição de sementes para juvenis, isso gera uma alta variação na proporção de cada classe na população conforme variamos o nível de perturbação. Em geral, a proporção do estágio semente na população decai e a proporção de jovens aumenta ligeiramente conforme a taxa de transição de sementes para juvenis aumenta. O estágio adulto é pouco afetado e permanece com uma proporção mais ou menos constante com a redução do nível de perturbação (aumento da taxa de transição de sementes para juvenis)A figura abaixo mostra isso mais claramente.
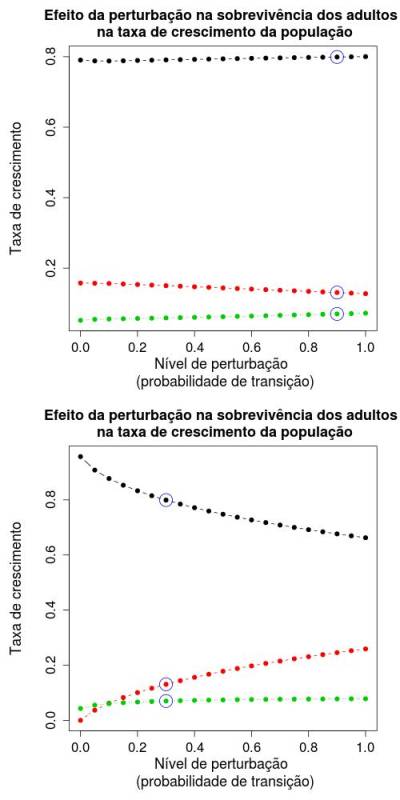
Os circulos azuis indicam a situação original da matriz de transição.
Exercício 5
Variando os valores de $h$ e $n$ (para valores positivos) estamos apenas variando a escala do gráfico, já que o padrão é o mesmo. Afinal, a função que estamos plotando é a mesma. Esses gráficos indicam que a nova probabilidade de sobrevivência denso-dependente varia não linearmente de acordo com os valores de $n$ e $h$. Ou seja, se mantivermos $h$ constante e variarmos apenas $n$, percebemos que a função de denso-dependência varia menos quanto mais aumentamos o $n$. Não só isso, seu valor vai diminuindo com o aumento de $n$, o que é intuitivo. Se invertermos o processo dá na mesma. Mantendo $n$ constante e variando somente $h$ percebe-se que aumentos em $h$ implicam em aumentos no valor da função de denso-dependência. Do mesmo modo, a função varia menos conforme aumentamos o valor de $h$ (espaços entre isoclinas aumenta). No final, isso quer dizer que aumentando $h$ estamos favorecendo a sobrevivência por torná-la mais próxima de seu valor máximo ($ \frac{h}{h+N} \to 1$). Já aumentando $n$ estamos desfavorecendo a sobrevivência em relação ao seu máximo (e esse é o efeito denso dependente que queremos; negativo nesse caso). Assim, $ \frac{h}{h+N} \to 0$.
Matematicamente o $h$ pode ser negativo, mas biologicamente isso não faz sentido. Neste modelo, $h$ pode ser considerado como um coeficiente que informa a intensidade de denso-dependência ou o quanto o aumento de um indivíduo do estágio considerado implica em uma redução na sobrevivência deste estágio. Deste modo, estamos considerando uma denso-dependência negativa. Contudo, se colocamos $h < 0$, poderíamos interpretar que a denso-dependência passaria a ser positiva. Mas isso não faz muito sentido aqui (essa função de denso dependência não é indicada se queremos modelar denso-dependência positiva).
Primeiramente, temos que ter claro que o valor final da sobrevivência dos adultos deve ser um valor entre 0 e 1. Desta forma, se $h < 0$ ou $ \frac{h}{h+N} < 0$ e teremos $P_{33} < 0$ ou $ \frac{h}{h+N} > 1$ o que torna possível, matematicamente, encontrarmos $P_{33} > 1$. Isso só não ocorrerá se $P'_{33} < \frac{h+n}{h}$, restringindo portanto os valores de $h$ negativo viáveis, o que aparentemente não faz sentido biológico.
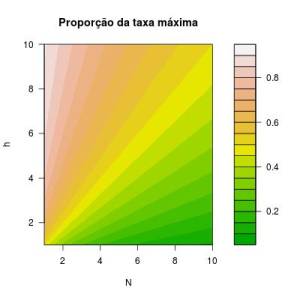
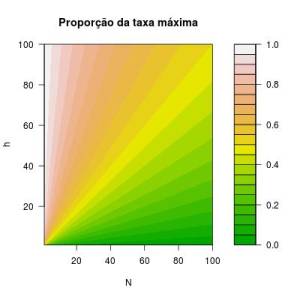
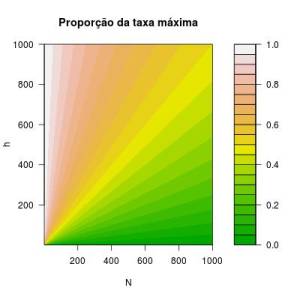
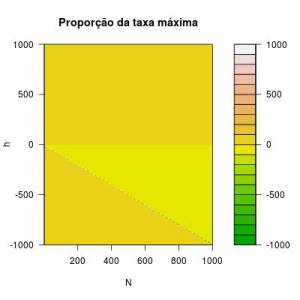
Figura 1 - Valor da função de denso-dependência em relação a valores de $n$ e $h$. Nos três primeiros gráficos, apenas variamos os valore de $n$ e $h$, para $h$ positivo. No ultimo gráfico, apresentamos os valores da função permitindo que $h$ seja negativo.
Exercício 6
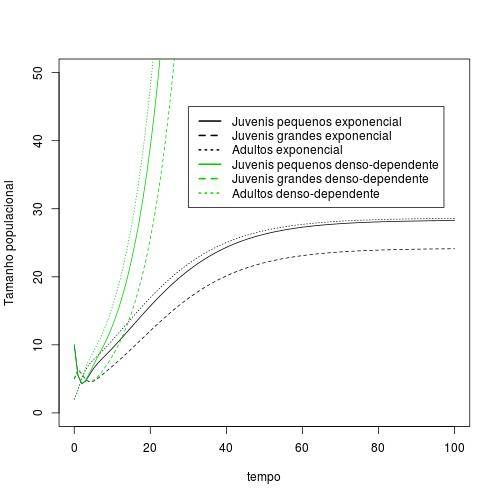
Visto que a denso-dependência leva a uma estabilidade do tamanho populacional (e de cada estágio separado), ao diminuir $h$ diminui-se o tamanho populacional na estabilidade. Por outro lado, aumentando $h$ aumentamos o tamanho populacional na estabilidade, sendo que para valores muito altos de $h$ o crescimento da população se assemelha por mais tempo a um crescimento exponencial. No entanto, sempre haverá a estabilização em um tamanho populacional que será tão maior quanto maior for $h$.
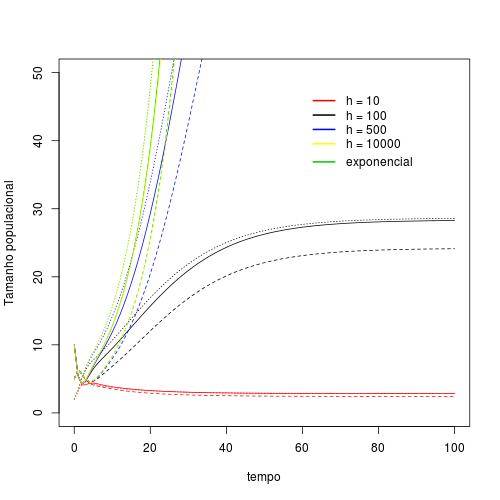
Em outra escala:
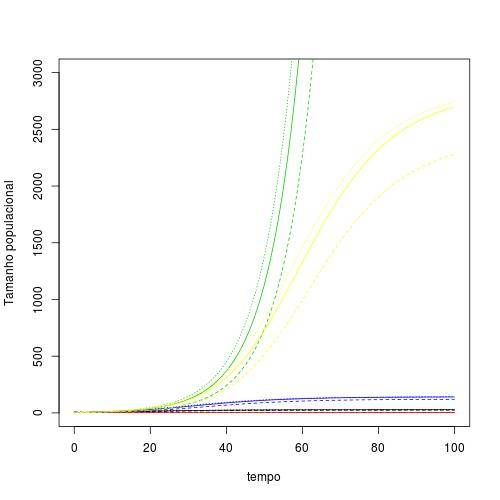
Há similaridade no sentido que independentemente das condições iniciais, o número de indivíduos de cada estágio tenderá a se estabilizar num mesmo valor, assim como no crescimento sem denso-dependencia as curvas exponenciais eram as mesmas, porém com um pequeno atraso para as populações que iniciam com menos individuos. Neste ultimo caso, não há um ponto de equilibrio estável em que a população chega após tempo suficiente. Mas espera-se que num tempo infinito as populações sejam iguais na ausência de denso dependencia, o que é semelhante o ocorrido no crescimento denso-dependente. Portanto, as condições iniciais não alteram o crescimento populacional com denso-dependência.
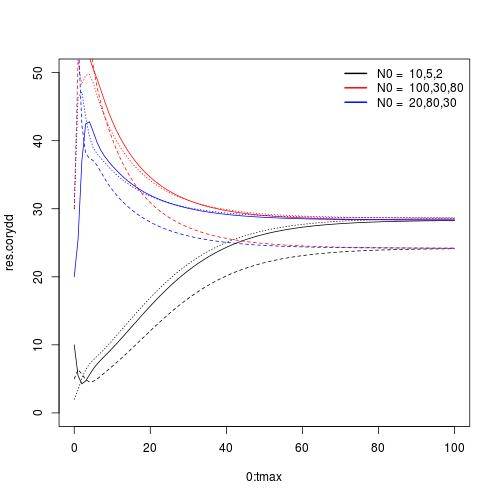
Exercício 7
O tempo para a estabilização das proporções será:
Juvenis pequenos = 17 anos(? Não sei a unidade de tempo)
Juvenis grandes = 13 anos
Adultos = 12 anos
Exercício 8
O aumento do valor reprodutivo encontrado se deve ao fato de estagios mais avançados (adultos) contribuirem mais para o crescimento populacional. Além disso, as sementes não se reproduzem, diminuindo o valor reprodutivo para esse estágio.
Códigos em R para esses exercícios