• $b$: é a taxa de crescimento intrínseco da população de presas. Neste caso assume-se um crescimento exponencial na ausência de predadores.
• $a$: é a taxa consumo de presas por indivíduo de predador. Mede o quanto um predador afeta negativamente o crescimento das presas (também chamado de eficiência de captura).
• $e$: é uma constante de conversão que diz o quanto de uma presa consumida se converte em indivíduos de predador
• $s$: é a taxa de mortalidade dos predadores. Neste caso assume-se um decaimento exponencial da população de predadores na ausência de presas.
  

Vale lembrar que $aV$ é a resposta funcional do predador e $eaV$ é a resposta numérica dos predadores.

• Quanto ao modelo com canibalismo, uma abordagem inicial (que depois se mostrou incoerente, como será evidenciado) foi substituir $P$ por $V$ nas duas equações (ou mesmo dar um outro nome para essas variáveis, $C$ por exemplo). Com isso teremos duas equações diferenciais que informariam como o número de indivíduos de uma espécie que comporta canibalismo varia no tempo. Aqui, algumas coisas vieram à mente. Primeiro, considerando apenas a primeira equação, percebemos que ela é a mesma que a equação de crescimento populacional logístico, o que responde a segunda parte do exercício.

$$ \frac{d}{dt}C = bC - aC^2 = rN -\frac{r}{K}N^2$$

onde $b = r$ e $\frac{r}{K} = a$.

Contudo, o que fazemos com a segunda equação? Pelo raciocínio inicial, a segunda equação também informaria $\frac {d}{dt} C$. Se considerássemos somente esta equação, obteríamos uma equação um pouco diferente da logística. Na realidade é a equação oposta à logistica, já que será:

$$\frac {d}{dt} C = eaC^2 - sC = $$ $$- \left(rN -\frac{r}{K}N^2 \right)$$ se $r = s$ e $\frac{r}{K} = ea$.

Ou ela seria igual à logistica se os parâmetros $s$ e $ae$ fossem negativos ($r = -s$ e $\frac{r}{K} = -ea$). Portanto, usando-se essa abordagem para estabelecer a analogia (apenas substituir $P$ por $V$ ou substituir tudo por $C$) não chegamos a resultados coerentes. Não me parece razoável considerar valores negativos dos parâmetros, assim como uma equação oposta à logistica gera crescimentos populacionais bem estranhos. Além disso, o que me pareceu mais incoerente é que em uma das equações $\frac{r}{K}$ teria que ser igual a $a$ e na outra igual a $ae$. Em suma, fazer essa analogia me parece furada.

Uma outra forma de ver essas inconsistências é considerando que se as duas equações geram os valores de $\frac {d}{dt} C$, elas são iguais. Então,

$$ bC - aC^2 = eaC^2 - sC$$ o que será válido apenas se $$ C = \frac{b+s}{a(1+e)}$$ Então, a funcionalidade deste sistema é bem restrita…

Desta forma, se uma analogia com o modelo Lotka-Volterra é pretendida, devemos “enquadrar” o novo modelo dentro das premissas do modelo Lotka-Volterra. Primeiramente, devemos considerar que a população da espécie é composta por dois grupos de indivíduos, os canibais e os não canibais. Caso contrário, não faria sentido usarmos duas equações para modelar o crescimento populacional da espécie como um todo. Segundo, estamos assumindo que canibal não come canibal e o crescimento dos canibais depende somente do quanto eles conseguem converter daquilo que ingeriram de não canibal em novos indivíduos canibais. Assim, canibal da origem a canibal e não canibal à não canibal. Então, vejamos as equações abaixo:

$ \frac{d}{dt}N_{NC} = bN_{NC} - aN_{NC}N_{C}$

$ \frac{d}{dt}N_{C} = eaN_{NC}N_{C} - sN_{C}$

Podemos agora considerar uma propriedade particular deste sistema: os “predadores” são canibais e, portanto , pertencem à mesma espécie. Assumindo isso, podemos dizer que a variação no tamanho populacional total ($N_{tot}$) ao longo do tempo será igual ao crescimento do grupo dos não canibais ($N_{NC}$) menos a mortalidade que os canibais ($N_{C}$) causam nos não canibais, mais o crescimento dos canibais menos a mortalidade intrínseca dos canibais. Simbolicamente,

$$ \frac{d}{dt}N_{tot} = \frac{d}{dt}N_{NC} + \frac{d}{dt}N_{C}$$ $$ \frac{d}{dt}N_{tot} = bN_{NC} - aN_{NC}N_{C} + eaN_{NC}N_{C} - sN_{C}$$ Agora sim podemos substituir $N_{NC}$ e $N_{C}$ por um nome comum, a fim de representá-los como da mesma espécie e dar sentido à equação diferencial acima. Isso faz com que,

$$ \frac{d}{dt}N = (b-s)N - a(1-e)N^2$$ que será igual a $$ \frac{d}{dt}N = rN - \frac{r}{K}N^2$$ se $r = b-s$ e $\frac{r}{K} = a(1-e)$. Isso sim faz muito mais sentido…

• Os pontos do gráfico representam as condições iniciais (número inicial de indivíduos de presas e predadores) para cada trajetória.

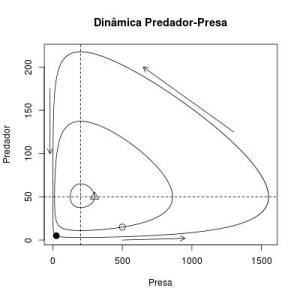
• As curvas sólidas representam como se comportam as trajetórias de presas e predadores ao longo do tempo para cada condição inicial averiguada. Cada ponto da trajetória dá o número de presas e o número de predadores num dado tempo. Como se percebe, este sistema é determinístico e neutramente estável (depende das condições iniciais).

• As linhas pontilhadas representam as isoclinas das presas (horizontal) e dos predadores (vertical). Ou seja, $ \frac{d}{dt}V = 0$ e $\frac{d}{dt}P = 0$.

• Este é um ponto de equilibrio do sistema, ou uma condição (valor de número de presa e de predador) que faz com que as duas equações diferenciais sejam iguais a 0. Este ponto de equilibrio é o que se chama de neutramente estável, pois por um lado as duas populações nunca chegam nele, a não ser que o sistema inicie nesse ponto (onde permanecerá para sempre). Dada uma condição inicial, as populações das duas espécies ficarão girando em torno deste ponto. O formato da trajetória dependerá destas condições iniciais, por isso ele não é totalmente estável (como num ciclo limite). Para cada condição inicial o sistema estabiliza com uma órbita diferente. Uma vez perturbado, o sistema caminhará na nova órbita que atinge até que uma nova perturbação ocorra.

• Considerando apenas isoclina das presas, ela indica as condições em que o crescimento das presas será nulo, o que ocorre quando o número de predadores = $b/a$ para qualquer número de presas no sistema. Então, se um ponto no diagrama estiver abaixo desta isoclina, significa que há menos predadores que o necessário para zerar o crescimento das presas. Portanto, o crescimento das presas será positivo e haverá uma tendencia de aumentos de número de presa num tempo posterior. Se o ponto estiver acima da isoclina, o inverso ocorre já que o número de predadores é superior ao necessário para anular o crescimento das presas e o crescimento das presas será negativo (decrescimento da população de presas).
  

O mesmo raciocínio pode ser aplicado para a isoclina dos predadores. Neste caso, pontos à esquerda da isoclina representam regiões onde a população de predadores tem crescimento negativo e pontos à direita momentos em que os predadores estão em crescimento, pois o número de presas será respectivamente, menor e maior que o necessário para anular o crescimento (ou decrescimento) dos predadores. Em conjunto, as duas isoclinas dividem o diagrama em quatro quadrantes que indicam o caminho da dinâmica populacional das duas espécies para cada combinação de valores de predadores e presas no sistema num determinado momento. A resultante das tendências das presas e dos predadores em um determinado ponto do diagrama sempre aponta para o ponto de equilibrio neutramente estável. Por isso, o sistema é ciclico, e apresenta trajetórias orbitais (não sei se pode-se chamar essas figuras de elipse ???) ao redor do ponto de equilíbrio.

• O grande problema do modelo Lotka-Volterra continuo (original) é sua estabilidade neutra, uma vez que a ocorrência de alguma perturbação no sistema o leva a uma orbita diferente ao redor do ponto de equilibrio. Esta órbita permanece fixa até que uma nova perturbação ocorra e altere o estado do sistema. Ou seja, uma vez perturbado, o sistema não volta às suas condições iniciais na ausência de uma nova perturbação que o leve para algum ponto da órbita inicial.

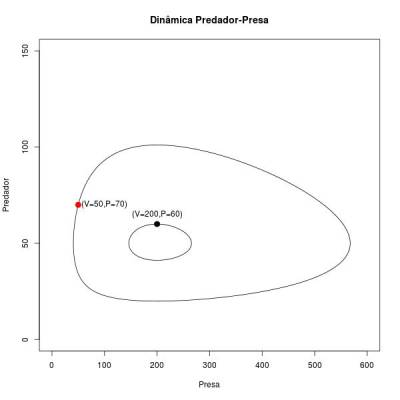
Já o modelo discreto de Lotka-Volterra com crescimento sincronico das populações leva o sistema à uma condição altamente instável. Como a tangente sempre aponta para fora da orbita, a cada passada (passagem de uma unidade de tempo) o sistema pula para uma orbita mais externa, até conduzir uma das populações à extinção. Se for a de presas primeiro, a de predador se extinguirá por consequência. Se for a de predador, a população de presas crescerá exponencialmente, pois não haverá o predador para regulá-la (ver figura abaixo).

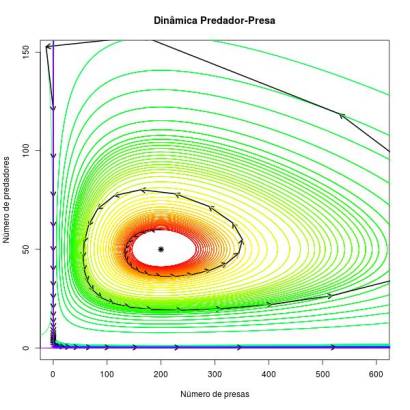
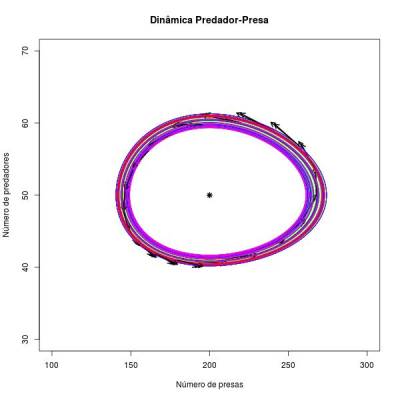
Por fim, no modelo discreto de Lotka-Volterra com crescimento assincronico, conforme avançamos no tempo o sistema alterna entre órbitas mais internas e orbitas mais externa que a que estava anteriormente. Em média as duas populações acabam flutuando ao redor da órbita dada pelas condições iniciais. Portanto, neste caso o sistema tende à estabilidade. Isso é percebido pelo fato das órbitas com cores diferentes estarem misturadas na situação assicrônica e seguir as cores do arco-iris (função rainbow no R) para a situação sincronica (ou seja, está sempre indo para uma órbita mais externa).


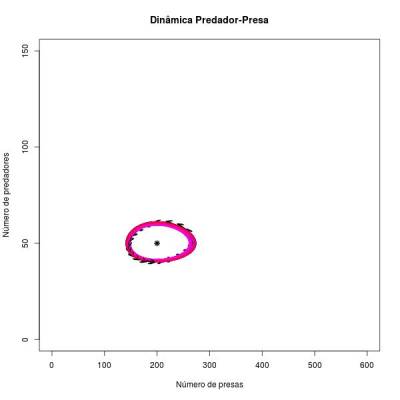Dando um zoom na imagem acima:

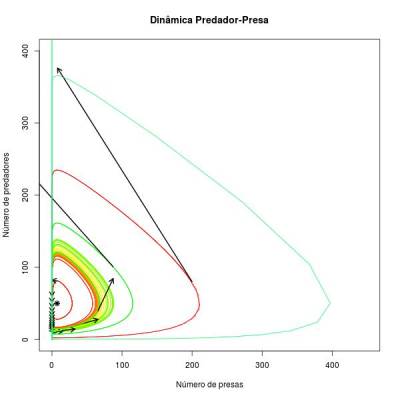
No entanto, mesmo no caso de assincronia, o sistema poderá eventualmente tomar um caminho que leve à extinção de uma das espécies ou das duas, o que dependerá dos valores dos parâmetros do modelo. Abaixo um exemplo em que $a = 0.032$, $b = 1.6$, $e = 0.6$ e $s = 0.14$.

Alterando o número de picos, estamos alterando a frequência com que o sistema pula de órbita. Ao considerarmos que a média de ruido é zero, isso quer dizer que no final, o quanto o sistema irá pular para órbitas mais externas, ele também irá pular na mesma magnitude para órbitas mais internas. Após todos os eventos estocásticos que ocorrem no tempo total de simulação, as duas populações tenderão em média a caminhar pela órbita inicial (determinada pelos valores iniciais de presas e predadores).

Devido à estocasticidade, o sistema pode, eventualmente, atingir uma órbita que leve à extinção de uma das populações. A probabilidade disso ocorrer será tão maior quanto maior for o desvio padrão do ruído, assim como dependerá da frequência com que o ruído ocorre (i.e. número de picos). A variabilidade de valores de presas e predadores que o sistema assume será maior quando o número de picos é intermediário em relação a quando o número de picos é muito baixo ou muito alto. Ou seja, há uma variação maior de trajatórias que ocorrem ao redor da órbita média quando a frequência de ruídos é intermediária. Isso se explica pelo fato de quando o número de picos é muito baixo, o sistema desvia poucas vezes de sua órbita média. Quando o número de picos é muito grande, o sistema desvia quase que constantemente da órbita média, o que impede que ele se desvie muito da órbita média. Finalmente, se o número de picos é intermediário, há a possibilidade de sistema desviar bastante da órbita média até que ele volte a valores mais próximos da média novamente.

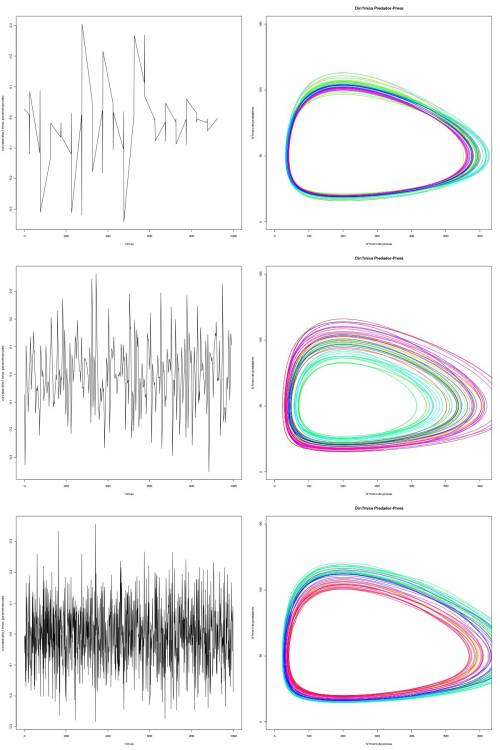
Figura 1 - Os gráficos da esquerda representam o ruído em funçao do tempo e os da direita o espaço de fase predador-presa. O número de picos = $20$, $200$ e $2000$, respectivamente a cada linha de gráficos da figura. O fato das cores estarem misturadas nos gráficos de espaço de fase evidenciam que o sistema pula para órbitas mais internas e mais externas a que se encontrava no tempo anterior sem seguir uma direção específica (e.g. sem pular sempre para órbitas externas).

• Neste gráfico, foi feito o espaço de fases das presas e dos predadores considerando a nova resposta funcional do modelo (Rosenzweig-MacArthur; resposta funcional Holling tipo II). Na abcissa está o número de presas e na ordenada o número de predadores. Neste caso, devido à inclusão do crescimento logistico na equação da variação das presas no tempo (em detrimento do crescimento exponencial do Lotka-Volterra clássico) e da nova resposta funcional, a isoclina das presas não é mais uma reta paralela ao eixo das presas e perpendicular à isoclina dos predadores. Essa isoclina será uma parábola. Isso indica que conforme aumenta o número de presas no sistema, o número de predadores necessários para anular o crescimento das presas aumenta até um pico e depois cai. Isso se deve ao efeito Allee dado pelo crescimento logistico da população de presas, assim como ao fato de que a eficiência do predador atinge um valor máximo; depois de um certo número de presas no sistema, a taxa de consumo de presas por número de presas disponíveis começa a cair pois os predadores não podem mais aumentar seu consumo linearmente com a disponibilidade de presas no sistema.
  

Considerando um diagrama de espaço de fases em que os predadores estão na ordenada e as presas na abcissa, as equações que definem as isoclinas das presas e dos predadores serão:

• Isoclina das presas

$$\frac{dV}{dt}= bV(1-\alpha V)- w \frac{VP}{D+V} = 0 $$ o que nos leva a duas soluções: $$ V = 0$$ que não nos interessa e $$ P(V) = \frac{b}{w} (1-\alpha V)(D+V)$$ que também pode ser escrita assim: $$ P(V) = \frac{bD}{w} + \frac {b(1-\alpha D)}{w}V- \frac{b \alpha}{w} V^2$$

• Isoclina dos predadores

$$ \frac{dP}{dt} = ew \frac{VP}{D+V} -sP = 0$$ que também nos leva a duas soluções: $$ P = 0$$ que não interessa e $$ V = \frac{sD}{ew-s}$$ Desta forma, a isoclina dos predadores não depende dos predadores. Isso implica que a isoclina dos predadores é uma reta paralela ao eixo dos predadores, implicando que existe apenas um tamanho da população de presas que leva o crescimento dos predadores a 0, para qualquer quantidade de predadores no sistema.

• Qualitativamente, o sistema de equações diferenciais proposto por Rosenzweig-MacArthur prevê duas soluções gerais: uma em que o sistema converge para um ciclo limite e outra em que o sistema converge para um ponto fixo. No entanto existem quatro soluções mais específicas, três que convergem para pontos fixos e uma que converge para ciclos limites. Como neste exercício a prática foi variar os valores da capacidade suporte das presas, apresentarei as condições para que essas quatro soluções de equilíbrio ocorram, dado em relação à capacidade suporte das presas. Mas antes disso, devo deixar claro como as condições serão obtidas.

Primeiro, uma situação chave é aquela em que a isoclina dos predadores cruza a isoclina das presas no ponto de pico da isoclina das presas (ponto de máxima da parábola). Nesta condição, o sistema começa a se comportar como um ciclo limite. Assim, o sistema tenderá a ciclos limite sempre que a isoclina dos predadores cruzar a isoclina das presas em pontos da isoclina de presas em que o número de presas é menor que o número de presas no ponto de pico (i.e. para trás do pico da parábola). Quanto mais afastado em direção ao eixo dos predadores for esse ponto de cruzamento, maior será a probabilidade do sistema atingir um ciclo limite em que ocorre a extinção de uma das espécies ou de ambas (a órbita do ciclo limite é muito grande, levando a um ponto de convergência [$(0,0)$ ou $(K,0)$, onde o primeiro valor é o número de presas e o segundo o número de predadores]).

Por outro lado, o sistema convergirá para um ponto fixo de coexistência estável das duas espécies sempre que a isoclina dos predadores cruzar a isoclina das presas em pontos da isoclina de presas em que o número de presas é maior que o número de presas no ponto de pico (i.e. para a frente do pico da parábola). No entanto, como veremos, há casos de combinação de parâmetros que fazem com que a isoclina das presas nunca cruze a isoclina dos predadores. Neste caso, o sistema convergirá para um ponto fixo estável com extinção dos predadores e com as presas na sua capacidade de suporte. Vejamos mais claramente essas situações:

• Determinando a situação chave

Para se saber a condição em que a isoclina dos predadores cruza a isoclina das presas no ponto de pico da isoclina das presas é simples. O pico da isoclina das presas é obtido igualando-se a derivada da isoclina a $0$ e substituindo o valor de $V$ nesta equação pelo valor de $V$ dado pela isoclina dos predadores. Então,

$ P(V) = \frac{bD}{w} + \frac {b(1-\alpha D)}{w}V- \frac{b \alpha}{w} V^2$

O que queremos é que

$ \frac{d}{dV}P = 0$. Se

$ \frac{d}{dV}P = \frac {b(1-\alpha D)}{w} - 2 \frac{b \alpha}{w} V = 0 $, teremos

$ \frac {b}{w}(1-\alpha D - 2 \alpha V) = 0$, levando a duas soluções:

$b=0$, que não nos interessa por se tratar de uma situação muito particular que leva à extinção das duas espécies, e:

$ 1-\alpha D - 2 \alpha V = 0 $ que resulta em

$$ \alpha = \frac{1}{2V+D}$$ Fazendo $V=\frac{sD}{ew-s}$, teremos a nossa condição em relação a $\alpha$ ou $K$, que será:

$$ \alpha = \frac{ew-s}{D(ew+s)}$$ $$ K = \frac{D(ew+s)}{ew-s}$$

Desta forma, se $K \ge \frac{D(ew+s)}{ew-s}$,

o sistema convergirá para um ciclo limite, cuja órbita será tão maior quanto maior for $K$. Haverá um valor de $K$ limite a partir do qual o sistema convergirá para o ponto de extinção das duas espécies. Nessas órbitas grandes, ocorrem situações em que o número de predadores cresce muito e extingue as presas, extinguindo-se posteriormente por falta de recursos que permitam seu crescimento. Isso é uma situação que se considera paradoxal (aumentando-se a capacidade suporte das presas estas se aproximam mais da extinção). Contudo, eu não soube estabelecer o valor exato de $K$ para a ocorrência dessa solução (i.e. extinção das duas espécies).

Por outro lado, se $K < \frac{D(ew+s)}{ew-s}$,

O sistema convergirá obrigatoriamente para um ponto fixo, que pode ser um ponto de coexistência das duas espécies ou o ponto em que há extinção dos predadores e as presas atingem sua capacidade suporte $(K,0)$. Enquanto $K < \frac{D(ew+s)}{ew-s}$ e as isoclinas estiverem se cruzando, o sistema convergirá para a primeira situação (coexistência estável). Já quando as isoclinas se cruzarem no ponto em que a isoclina das presas encosta no eixo das presas (que por sinal será = a $K$, como veremos) ou se essas isoclinas não se cruzarem, o sistema convergirá para a segunda situação (ponto $(K,0)$). Então, precisamos determinar as condições em que as isoclinas se cruzam no ponto em que a isoclina das presas encosta no eixo das presas. Isso ocorrerá quando a equação da isoclina das presas for igual a $0$. Sendo:

$ P(V) = \frac{b}{w} (1-\alpha V)(D+V) = 0 $, haverão três soluções para essa equação.

$b = 0$, que não nos interessa,

$ D = -V$, que não existe (não pertence ao domínio de nosso sistema), e $ 1- \alpha V = 0$. Neste caso,

$$ V = \frac{1}{\alpha}$$ $$ V=K$$

Como a isoclina dos predadores deve cruzar nesse ponto, ou cruzar o eixo das presas num ponto em que o número de presas é maior que $K$, chegaremos às seguintes condições:

$ V=K=\frac{sD}{ew-s}$.

Se $K \le \frac{sD}{ew-s}$, os sistema convergirá para o ponto fixo $(K,0)$.

Se $ \frac{sD}{ew-s} \le K < \frac{D(ew+s)}{ew-s}$, então o sistema convergirá para um ponto fixo de coexistência das duas espécies.

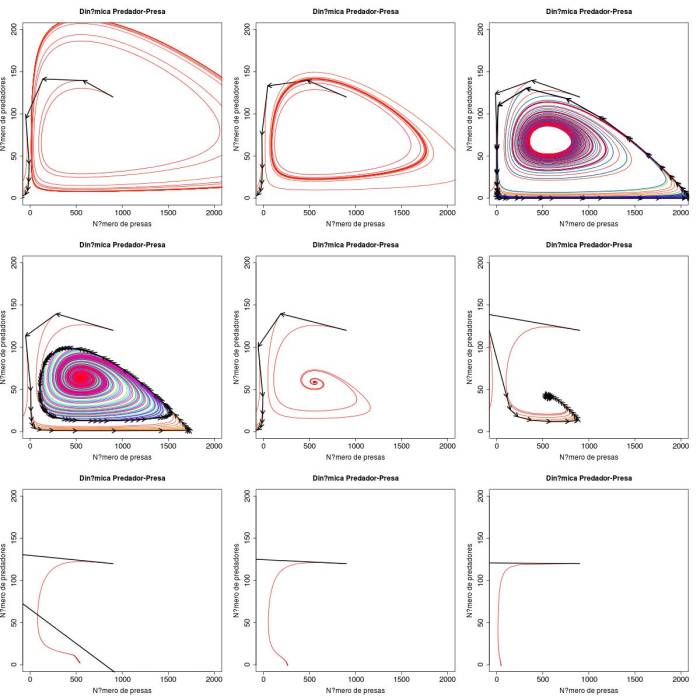
Devemos ter em mente que soluções que envolvem pontos fixos são de certa forma indesejáveis, já que na natureza é muito improvável que as duas populações (presas e predadores) se estabilizem em um único valor. Abaixo são apresentados os diagramas de espaço de fase para cada um dos casos apresentados acima.

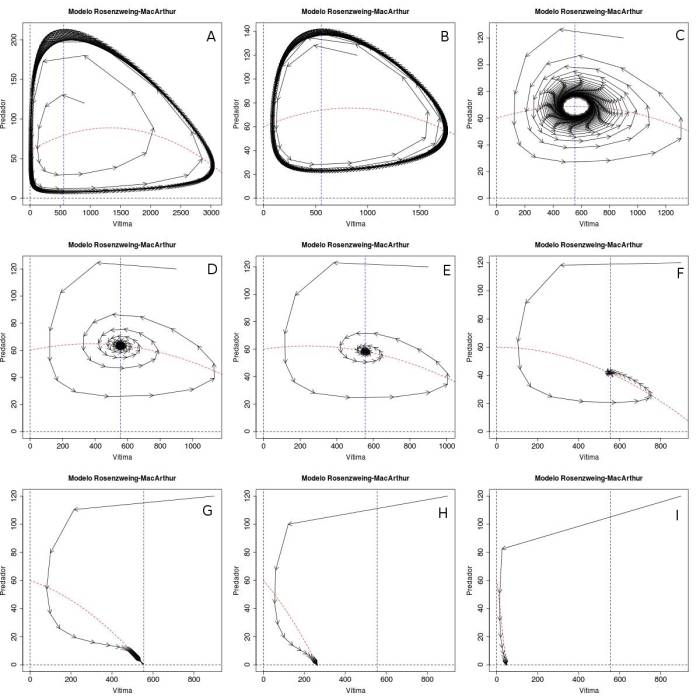Figura 1 Espaços de fase representando as quatro soluções para o sistema de Rosenzweig-MacArthur. A) Ciclo limite levando as duas populações à extinção ($K=3654$). B) ciclo limite com coexistência estável ($K=2676$), C) ciclo limite com coexistência estável ($K=\frac{D(ew+s)}{ew-s}=2111$), D) a F) Ponto fixo com coexistência estável das duas espécies ($K=1743, 1484$ e $1000$, respectivamente), G) ponto fixo com extinção dos predadores e presas na capacidade suporte ($K = \frac{D(ew+s)}{ew-s} = 556$, H) e I) ponto fixo com extinção dos predadores e presas na capacidade suporte ($K = 263$ e $46$, respectivamente).

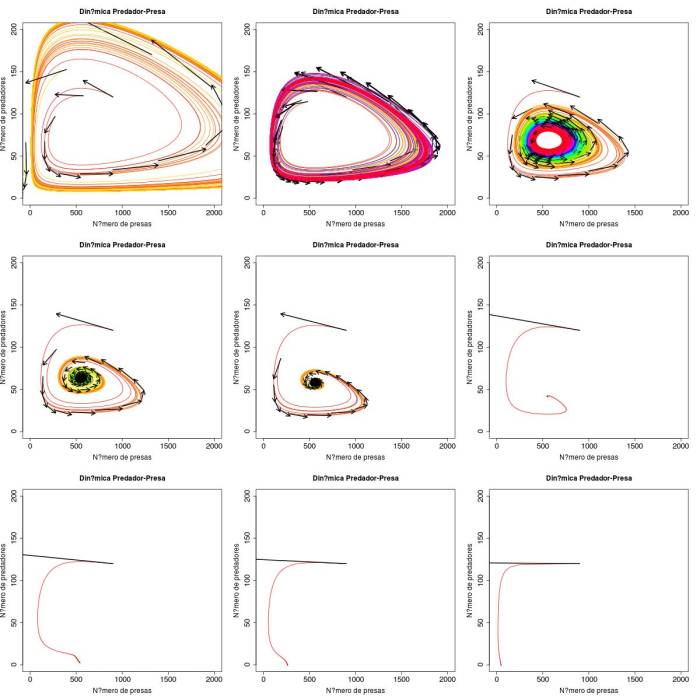
• Os gráficos abaixo representam dois conjuntos. O primeiro para dinâmica sincronica e o segundo para assincronica. Os valores de capacidade suporte são os mesmos da questão anterior. Percebe-se primeiro que para ambos os modelos, o caso em que as isolinhas não se cruzam nunca é solucionado. Para os outros casos, o modelo sincronico se comporta pior que o assincronico (como previsto anteriormente), mas ainda não resolve todos nossos problemas. O modelo sincronico leva a órbitas mais externas que invariávelmente levam o sistema para a extinção das espécies. O modelo assincrônico é melhor mais ainda permite que o sistema vá para um estado fixo com extinção de uma ou as duas espécies. Na verdade nenhuma dessas alternativas parece melhor que a do modelo continuo.

Códigos em R usados para estes exercícios.