VI) MODELOS DE DINÂMICA POPULACIONAL COM COMPETIÇÃO INTERESPSCÍFICA
Exercício 1
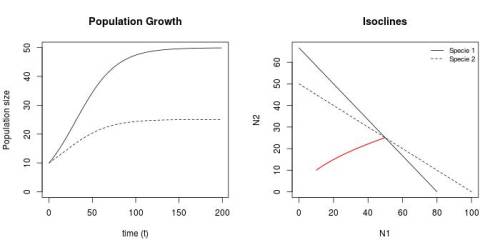
Figura 1 - Crescimento e espaço de fase das duas populações ($N_1(0)=10$, $N_2(0)=10$, $r_1=0.05$, $r_2=0.03$, $k_1=80$, $k_2=50$, $\alpha =1.2$, $\beta =0.5$) para tempo de observação = 200.
As isoclinas se cruzam, o que indica que as espécies podem coexistir ou que uma delas será excluida. A ocorrência de coexistência ou exclusão dependerá dos valores de $\alpha$, $\beta$ e $\frac{K_1}{K_2}$. No caso de exclusão, não se sabe a priori qual delas será excluída. Isso dependerá das condições iniciais do sistema ($N_1(0)$ e $N_2(0)$), assim como da relação entre $r_1$ e $r_2$.
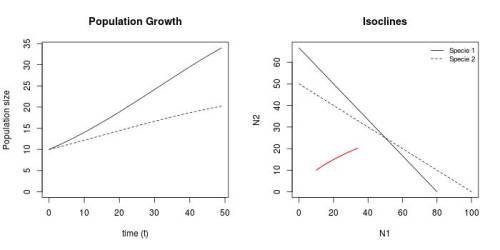
Figura 2 - Crescimento e espaço de fase das duas populações (mesmos valores dos parâmetros de fig.1) para tempo de observação = 50.
Observando o gráfico do crescimento populacional das duas espécies não é possível predizer com certeza se as espécies coexistirão. Neste cenário, ainda estamos no período de transiente e nenhuma das populações se estabilizaram. Apesar de ambas estarem crescendo, não podemos dizer com clareza se com mais tempo de observação, uma das populações não inverterá seu crescimento em direção à $N_i(t) = 0$.
Contudo, observando o espaço de fase esta incerteza se desfaz. Apesar de ainda nos encontrarmos numa fase de transiente, percebemos pelo gráfico que as condições de coexistência se satisfazem. Primeiramente, as isoclinas se cruzam. Além disso, percebe-se que $K_2<\frac {K_1}{\alpha}$, o que indica que as espécies tenderão a crescer até o ponto de equilíbrio estável indicado pelo ponto de cruzamento das isoclinas. Esse ponto será um atrator do sistema, nessas condições. Com isso, constatamos que o espaço de fase é muito importante para avaliações qualitativas do sistema.
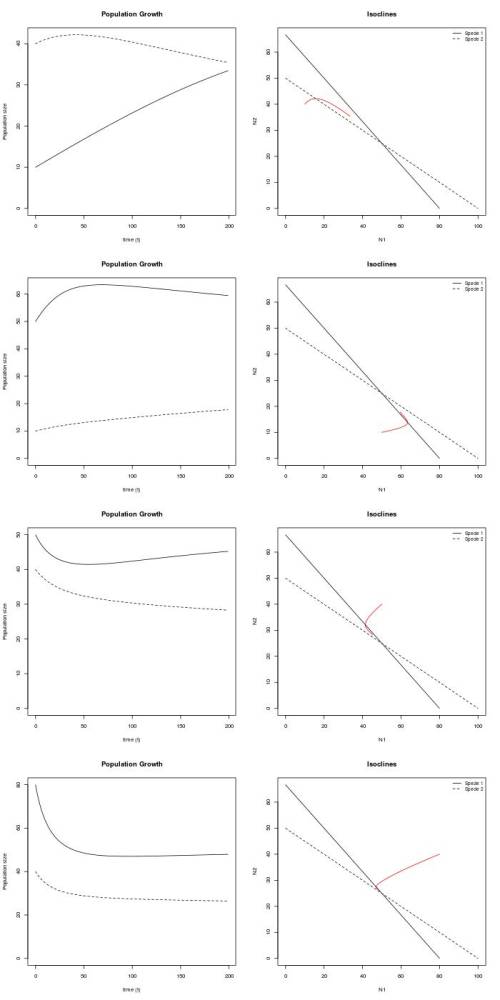
Figura 3 - Crescimento e espaço de fase das duas populações considerando diferentes condições iniciais ($N_1(0)=$ $10, 50, 50, 80$ e $N_2(0) = 40, 10, 40, 40$, respectivamente às linhas da figura) para tempo de observação = 200.
O uso de condições iniciais distintas não alteram os resultados previstos nas questões anteriores. Isso porque os pontos de equilíbrio permanecem os mesmos e a tendência das duas populações também. Como observado anteriormente, as condições de estabilidade do sistema dependerão de $N_1(0)$ e $N_2(0)$ somente no cenário em que
que as isoclinas se cruzam, mas $K_2>\frac {K_1}{\alpha}$. Neste caso, o ponto de equilibrio dado pelo cruzamento das isoclinas será instável (seria um repulsor???) e as populações tenderão a se excluir. Qual população é excluída dependerá de uma combinação de valores de $N_1(0)$, $N_2(0)$, $r_1$ e $r_2$.
Para que a uma das espécies sempre vençam, independentemente das condições iniciais, as isoclinas não podem se cruzar no primeiro quadrante do espaço de fase. Então, para a espécie 1 sempre vencer, precisamos que $\alpha < \frac{K_1}{K_2}$ e que $\frac{1}{\beta} < \frac{K_1}{K_2}$. Para a espécie 2 sempre vencer, basta invertermos as desigualdades ($\alpha > \frac{K_1}{K_2}$ e que $\frac{1}{\beta} > \frac{K_1}{K_2}$). Para que uma das espécies vençam, dependendo das condições iniciais (exclusão com equilibrio instável), precisamos que $\alpha > \frac{K_1}{K_2}$ e que $\frac{1}{\beta} < \frac{K_1}{K_2}$. Por fim, para que haja coexistência das duas espécies (equilíbrio estável), precisamos que $\alpha < \frac{K_1}{K_2}$ e que $\frac{1}{\beta} > \frac{K_1}{K_2}$. São dados alguns exemplos abaixo. Mantive os mesmos valores de $k_1$, $k_2$, $r_1$ e $r_2$ das primeiras questões, variando somente os valores de $\alpha$ e $\beta$, e de $N_1(0)$ e $N_2(0)$ apenas no ultimo caso, para representar a situação de equilibrio instável em que a espécie 2 exclui a espécie 1.
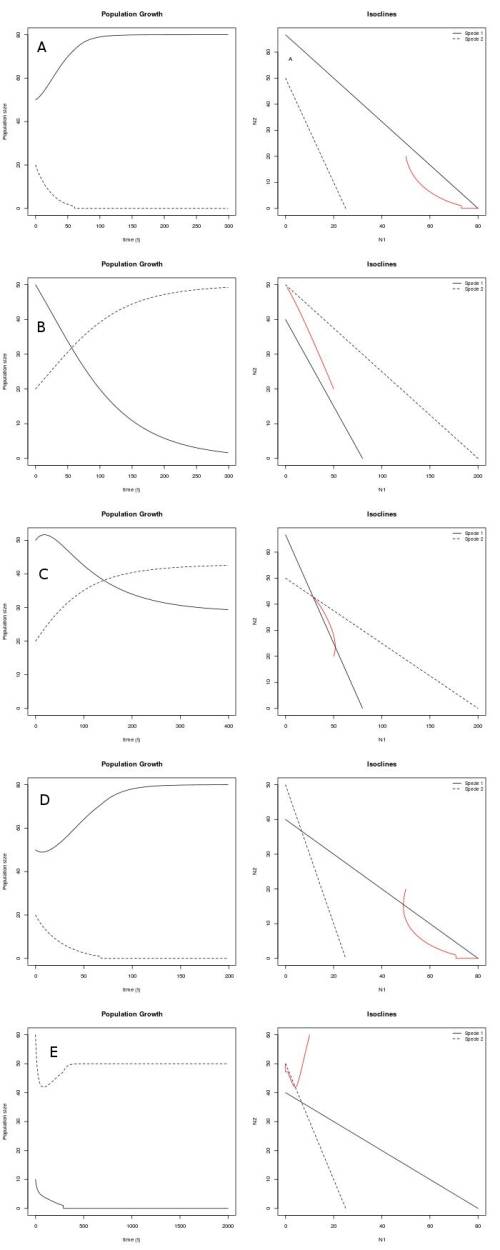
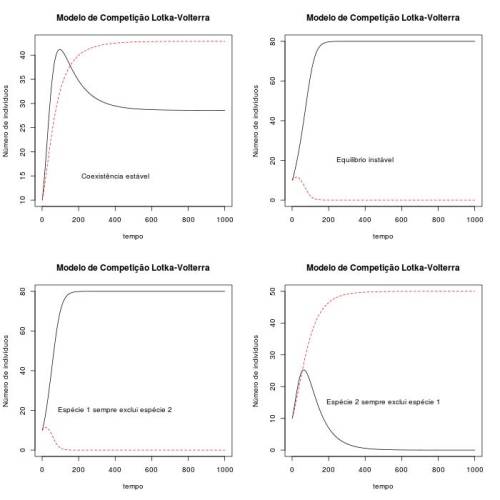
Figura 4 - Crescimento e espaço de fase das duas populações considerando diferentes cenários que podem ser previstos para o modelo de competição interespecífica ($N_1(0)= 50$ e $N_2(0) = 20$, exceto em E, em que $N_1(0)= 10$ e $N_2(0) = 60$. $k_1=80$, $k_2=50$, $r_1=0.05$ e $r_2=0.03$. A) Espécie 1 sempre exclui espécie 2 ($\alpha = 1,2$ e $\beta = 2$), B) Espécie 2 sempre exclui espécie 1 ($\alpha = 2$ e $\beta = 0.25$), C) Coexistência, equilíbrio estável ($\alpha = 1,2$ e $\beta = 0,25$), D) e E) Equilibrio instável ($\alpha = 2$ e $\beta = 2$). A espécie 1 exclui a espécie 2 com as condições iniciais de D) e o contrário ocorre com as condições iniciais de E.
Para interpretarmos a situação de coexistência entre as espécies, não vejo outra forma se não adotarmos as idéias que foram exploradas no exercício 4. Compreender esta situação em termos de razão entre as capacidades suporte não me faz muito sentido se não interpretarmos a capacidade suporte como uma constante relacionada à competição intra-específica de cada espécie ($K = \frac{1}{\alpha_{intra}}$). Ou seja, se a quantidade de recursos é fixa e homogeneamente distribuída no sistema, uma espécie que tem maior capacidade suporte que uma outra espécie consegue explorar os recursos mais “eficientemente” ou com uma menor competição entre seus indivíduos em relação à outra espécie. Ou seja, a competição intra-específica será maior para a outra espécie.
Dado isso, a coexistência entre duas espécies ocorrerá quando a competição entre as espécies for menor que a competição intra-específica. Considerando que $\alpha$ e $\beta$ representam quantos individuos de uma espécie são perdidos pela presença de um indivíduo da outra espécie, eles nos dão uma idéia do efeito competitivo de uma espécie sobre a outra. Se esses valores forem menores que a razão entre a competição intra-específica da espécie e a competição intra-específica da outra espécie teremos coexistência das espécies. Em outras palavras, isso quer dizer que se a competição intra-específica para uma espécie 1 for maior que para um outra espécie 2, mas se o efeito de 1 sobre a espécie 2 for proporcionalmente maior do que o efeito da espécie 2 sobre a espécie 1, haverá coexistência. Então, um menor crescimento intrínseco de uma espécie será compensado por uma maior redução que ela provoca na outra espécie, mantendo os níveis da outra espécie mais baixos do que seu potencial, o que por sua vez, faz com que o efeito desta outra espécie seja pequeno na espécie de menor crescimento intrínseco, permitindo que ela continue crescendo. Ambas as populações atingirão um equilíbrio estável com menos indivíduos em relação ao que teriam na ausência da outra espécie.
Exercício 2
Os valores dos parâmetros seguem os do exercício 1 quando avaliamos cada um dos cenários, sendo que para o caso de equilíbrio instável, usei apenas o caso em que a espécie um prevalece sobre a espécie 2.
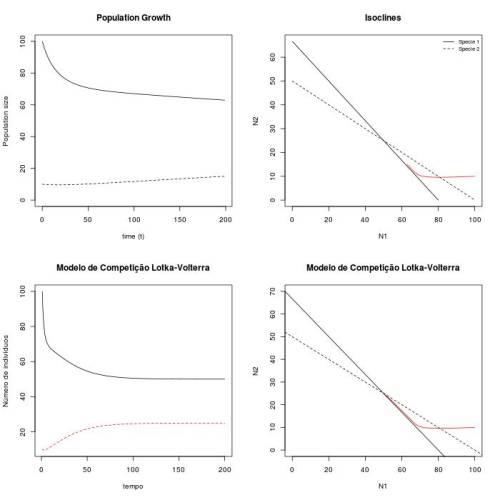
Os gráficos, para t=200 parecem um pouco diferentes uma vez que no modelo continuo as duas populações se encontram mais próximas ao seus respectivos pontos de estabilidade. Isso significa que no modelo discreto parece haver um transiente maior até se atingir a estabilidade. Isso é constatado pelo diagrama de espaço de fase, onde se pode observar que o tamanho das duas populações tendem ao ponto de equilíbrio estável do sistema. Ao diminuirmos o tempo máximo de observação (t = 5), o mesmo padrão é observado, exceto que é muito mais incerto prevermos a coexistência das duas populações analisando apenas o gráfico de $N(t) × t$. Neste caso, mesmo o modelo contínuo não permite inferências conclusivas sobre a estabilidade do sistema e sua situação final.
$$ t = 200$$
$$ t = 5$$
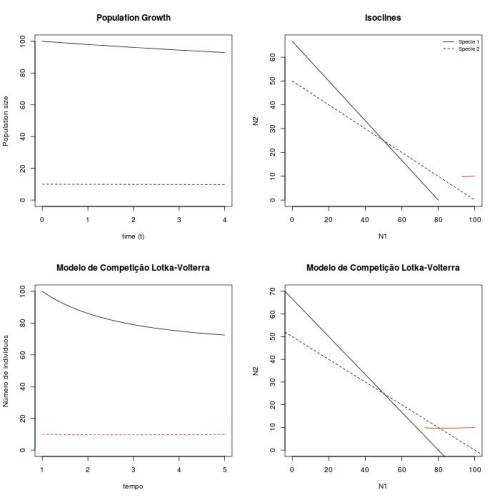
Exercício 3
Se três espécies estiverem competindo entre si, poderiamos esperar também todas as possibilidades. Contudo, determinar as situações de equilibrio e de estabilidade fica bem mais difícil devido ao aumento considerável do número de parâmetros do sistema de equações. Ao incluir uma terceira espécie ao modelo tradicional de competição,estamos inserindo 6 parâmetros adicionais, referentes à competição da espécie nova adicionada com cada uma das outras duas, mais a taxa de crescimento e a capacidade de suporte da terceira espécie.
Se as três espécies afetarem fortemente uma das outras duas espécies e serem afetadas fortemente por uma outra espécie diferente daquela a qual ela afeta fortemente; e se ao dizer afetar fortemente estou dizendo que a competição interespecífica é mais forte que a competição intra específica para aquela dada relação, eu espero que nessa situação haja coexistência das espécies, pois intuitivamente penso que o efeito negativo de uma espécie sobre uma segunda espécie é balanceado pelo efeito negativo da terceira espécie sobre a primeira. No fim, nenhuma espécie consegue ter densidade suficiente para eliminar nenhuma outra do sistema.
As equações deste sistema ficam assim:
$$ \frac{d}{dt}N_1(t) = r_1N_1(t) \left(\frac{K_1-N_1-\alpha N_2 - \gamma N_3}{K_1}\right)$$
$$ \frac{d}{dt}N_2(t) = r_2N_2(t) \left(\frac{K_2-N_2-\beta N_1 - \delta N_3}{K_2}\right)$$
$$ \frac{d}{dt}N_3(t) = r_3N_3(t) \left(\frac{K_3-N_3-\theta N_1 - \lambda N_2}{K_3}\right)$$
Exercício 4
$\alpha_{11}$ pode ser interpretado biologicamente como uma “taxa” de competição intra-específica, ou como cada indivíduo da espécie 1 afeta seu próprio crescimento. Da mesma forma, $\alpha_{22}$ tem a mesma interpretação para a espécie 2.
$\frac{d}{dt}N_2(t) = r_2N_2(t) \left [1-\alpha_{22}(N_2(t)+\beta N_1(t))\right]$
Essencialmente, nada muda. Os gráficos são iguais aos do exercício 2, o que é esperado e trivial. O que deve-se atentar é que agora os valores de $\alpha_{11}$ ou $\alpha_{22}$ estão em outra escala em relação aos de $K_1$ ou $K_2$. Claro, um é o inverso do outro. Igualmente, as unidades são diferentes (<indivíduo> para $K$ e <1/indivíduo> para $\alpha_{ii}$). Como os gráficos são os mesmos, apresento apenas o referente ao cenário de coexistência das espécies.
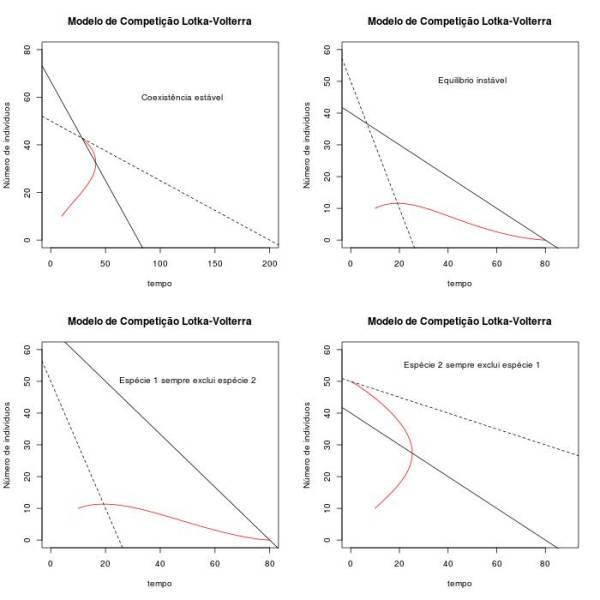
$\frac{d}{dt}N_2(t) = r_2N_2(t) \left [1-\alpha_{22}(N_2(t)+\alpha_{21}N_1(t))\right]$
Situação 1: Espécie 1 sempre exclui a espécie 2
$\alpha_{12} < \frac{K_1}{K_2}$ ; $\frac{1}{\alpha_{21}} < \frac{K_1}{K_2}$
$\alpha_{12} < \frac{\alpha_{22}}{\alpha_{11}}$ ; $\frac{1}{\alpha_{21}} < \frac{\alpha_{22}}{\alpha_{11}}$
Situação 2: Espécie 2 sempre exclui a espécie 1
$\alpha_{12} > \frac{K_1}{K_2}$ ; $\frac{1}{\alpha_{21}} > \frac{K_1}{K_2}$
$\alpha_{12} > \frac{\alpha_{22}}{\alpha_{11}}$ ; $\frac{1}{\alpha_{21}} > \frac{\alpha_{22}}{\alpha_{11}}$
Situação 3: Coexistência
$\alpha_{12} < \frac{K_1}{K_2}$ ; $\frac{1}{\alpha_{21}} > \frac{K_1}{K_2}$
$\alpha_{12} < \frac{\alpha_{22}}{\alpha_{11}}$ ; $\frac{1}{\alpha_{21}} > \frac{\alpha_{22}}{\alpha_{11}}$
Situação 4: Equilibrio instável (alguma das duas espécies exclui a outra)
$\alpha_{12} > \frac{K_1}{K_2}$ ; $\frac{1}{\alpha_{21}} < \frac{K_1}{K_2}$
$\alpha_{12} > \frac{\alpha_{22}}{\alpha_{11}}$ ; $\frac{1}{\alpha_{21}} < \frac{\alpha_{22}}{\alpha_{11}}$
Os gráficos para essas situações foram apresentados ao longo do exercício ( Código em R).