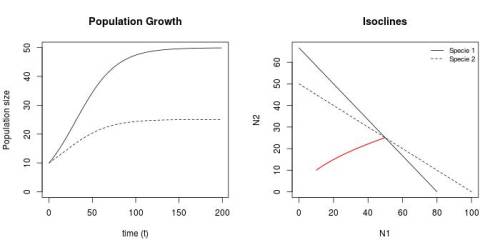
Figura 1 - Crescimento e espaço de fase das duas populações ($N_1(0)=10$, $N_2(0)=10$, $r_1=0.05$, $r_2=0.03$, $k_1=80$, $k_2=50$, $\alpha =1.2$, $\beta =0.5$) para tempo de observação = 200.

• As isoclinas se cruzam, o que indica que as espécies podem coexistir ou que uma delas será excluida. A ocorrência de coexistência ou exclusão dependerá dos valores de $\alpha$, $\beta$ e $\frac{K_1}{K_2}$. No caso de exclusão, não se sabe a priori qual delas será excluída. Isso dependerá das condições iniciais do sistema ($N_1(0)$ e $N_2(0)$), assim como da relação entre $r_1$ e $r_2$.
  

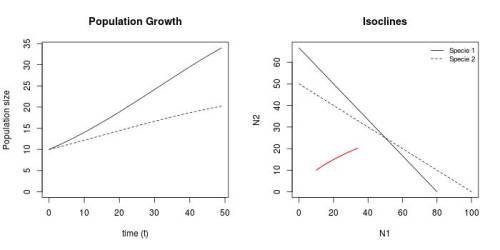
Figura 2 - Crescimento e espaço de fase das duas populações (mesmos valores dos parâmetros de fig.1) para tempo de observação = 50.

Observando o gráfico do crescimento populacional das duas espécies não é possível predizer com certeza se as espécies coexistirão. Neste cenário, ainda estamos no período de transiente e nenhuma das populações se estabilizaram. Apesar de ambas estarem crescendo, não podemos dizer com clareza se com mais tempo de observação, uma das populações não inverterá seu crescimento em direção à $N_i(t) = 0$.

Contudo, observando o espaço de fase esta incerteza se desfaz. Apesar de ainda nos encontrarmos numa fase de transiente, percebemos pelo gráfico que as condições de coexistência se satisfazem. Primeiramente, as isoclinas se cruzam. Além disso, percebe-se que $K_2<\frac {K_1}{\alpha}$, o que indica que as espécies tenderão a crescer até o ponto de equilíbrio estável indicado pelo ponto de cruzamento das isoclinas. Esse ponto será um atrator do sistema, nessas condições. Com isso, constatamos que o espaço de fase é muito importante para avaliações qualitativas do sistema.

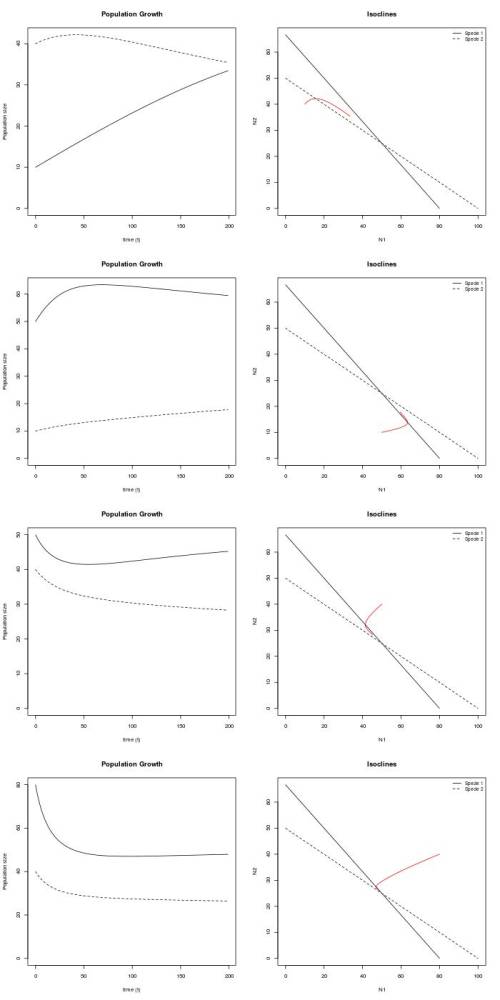
Figura 3 - Crescimento e espaço de fase das duas populações considerando diferentes condições iniciais ($N_1(0)=$ $10, 50, 50, 80$ e $N_2(0) = 40, 10, 40, 40$, respectivamente às linhas da figura) para tempo de observação = 200.

O uso de condições iniciais distintas não alteram os resultados previstos nas questões anteriores. Isso porque os pontos de equilíbrio permanecem os mesmos e a tendência das duas populações também. Como observado anteriormente, as condições de estabilidade do sistema dependerão de $N_1(0)$ e $N_2(0)$ somente no cenário em que que as isoclinas se cruzam, mas $K_2>\frac {K_1}{\alpha}$. Neste caso, o ponto de equilibrio dado pelo cruzamento das isoclinas será instável (seria um repulsor???) e as populações tenderão a se excluir. Qual população é excluída dependerá de uma combinação de valores de $N_1(0)$, $N_2(0)$, $r_1$ e $r_2$.

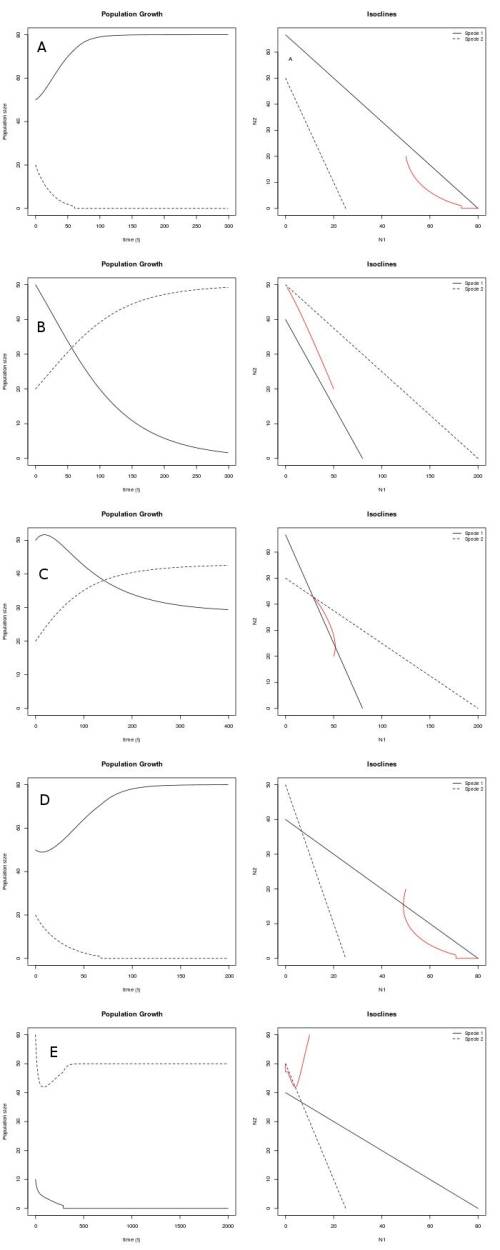
• Para que a uma das espécies sempre vençam, independentemente das condições iniciais, as isoclinas não podem se cruzar no primeiro quadrante do espaço de fase. Então, para a espécie 1 sempre vencer, precisamos que $\alpha < \frac{K_1}{K_2}$ e que $\frac{1}{\beta} < \frac{K_1}{K_2}$. Para a espécie 2 sempre vencer, basta invertermos as desigualdades ($\alpha > \frac{K_1}{K_2}$ e que $\frac{1}{\beta} > \frac{K_1}{K_2}$). Para que uma das espécies vençam, dependendo das condições iniciais (exclusão com equilibrio instável), precisamos que $\alpha > \frac{K_1}{K_2}$ e que $\frac{1}{\beta} < \frac{K_1}{K_2}$. Por fim, para que haja coexistência das duas espécies (equilíbrio estável), precisamos que $\alpha < \frac{K_1}{K_2}$ e que $\frac{1}{\beta} > \frac{K_1}{K_2}$. São dados alguns exemplos abaixo. Mantive os mesmos valores de $k_1$, $k_2$, $r_1$ e $r_2$ das primeiras questões, variando somente os valores de $\alpha$ e $\beta$, e de $N_1(0)$ e $N_2(0)$ apenas no ultimo caso, para representar a situação de equilibrio instável em que a espécie 2 exclui a espécie 1.
  

Figura 4 - Crescimento e espaço de fase das duas populações considerando diferentes cenários que podem ser previstos para o modelo de competição interespecífica ($N_1(0)= 50$ e $N_2(0) = 20$, exceto em E, em que $N_1(0)= 10$ e $N_2(0) = 60$. $k_1=80$, $k_2=50$, $r_1=0.05$ e $r_2=0.03$. A) Espécie 1 sempre exclui espécie 2 ($\alpha = 1,2$ e $\beta = 2$), B) Espécie 2 sempre exclui espécie 1 ($\alpha = 2$ e $\beta = 0.25$), C) Coexistência, equilíbrio estável ($\alpha = 1,2$ e $\beta = 0,25$), D) e E) Equilibrio instável ($\alpha = 2$ e $\beta = 2$). A espécie 1 exclui a espécie 2 com as condições iniciais de D) e o contrário ocorre com as condições iniciais de E.

• O