Equações diferenciais ordinárias são equações cuja a incógnita é a uma função. Ela se chama ordinaria pois a função diferenciada possui apenas uma variável e é sobre ela que se aplica a diferenciação. Isso distingue esse grupo de outros tipos de equações diferenciais como, por exemplo, as equações diferenciais parciais, paras as quais são diferenciadas derivadas parciais. Simbolicamente, isso pode ficar mais claro.

EQUAÇÃO DIFERENCIAL ORDINÁRIA (ODE)

$$ \frac{d}{dx}f(x)dx = Kf(x) $$

EQUAÇÃO DIFERENCIAL PARCIAL (PDE)

$$ \frac{d}{dx}f(x,t)dx = f(x)g(x)$$

A equação diferencial em questão é:

Assim, pelo método de Euler podemos calcular o valor esperado de $N(t)$ em intervalos de tempo ($\Delta t$) regulares e plotar esses valores em função do respectivo tempo. Esse calculo se procede da seguinte forma:

$ \frac{d}{dt}N(t) = \lim_{\Delta t \to 0} \frac{N_{t+\Delta t} - N_t}{\Delta t}$

Como nesse limite $\Delta t \to 0$ devemos realizar o calculo para intervalos de tempo o menor possível. Quanto menor o $\Delta t$ maior precisão teremos na solução. Além disso, devemos considerar os valores iniciais dos parâmetros, neste caso $r$ e $N(t)$ para $t=0$ ($N(0)$ ou $N_0$). Esses valores no tutorial eram:

$N_0=20$ e $r=2$.

Desta forma a resposta para o exercício 1 encontra-se no gráfico abaixo (optei por mostrar graficamente ao invés de uma tabela; se necessário posso colocar isso no codigo de R utilizado neste exercício).




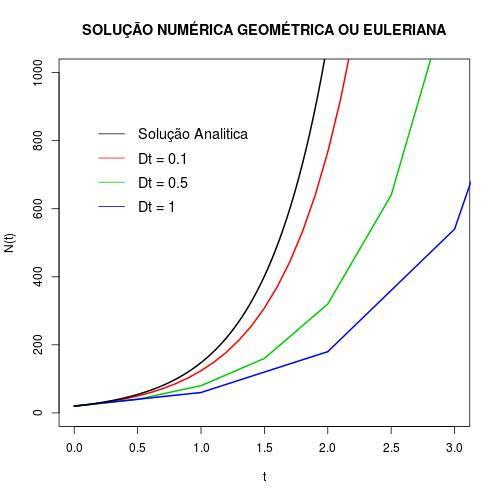
Código em R usado nesse exercício.

• 1)

• 2) $ \frac{d}{dt}m(t) = f(t)$
  

$ dm(t)=f(t)dt$

$\int^m dm = \int f(t)d(t)$

Então, a solução geral da equação 3 é: $$m(t)=\int f(t)d(t)$$

• 3) $ m(t)=\int f(t)d(t)$

$m(t)= \int a+b$ e$^{-ht}dt$

$m(t)=\int adt + \int b$ e$^{-ht}dt$

$$m(t)= at - \frac{b}{h} e^{-ht}$$

• 4) Esta etapa é o processo inverso para confirmar a solução da equação diferencial encontrada.
  

$m(t)= at - \frac{b}{h}$ e$^-ht$

$m(t)=g(t)-k(t)(h(j(t)))$

$ \frac{d}{dt}m(t)= g'(t) - k(t)[j'(t)h'(j(t))]-k'(t)(h(j(t))$

$\frac{d}{dt}m(t)= a - (-\frac{b}{h}(-h \exp^{-ht})) + 0=a-b$e$^{-ht}$