A teoria de amostragem de SADs define as abundâncias das espécies em uma amostra tomada de uma comunidade como o resultado de dois processos:

• A distribuição de abundâncias na comunidade
• A distribuição dos indivíduos nas amostras

Os detalhes teóricos estão na página de descrição geral do Projeto SADs.

Este tutorial em R simula amostragens de uma comunidade, para tornar mais concreta a lógica da teoria.

Vamos imaginar uma comunidade de 200 espécies, cujas abundâncias podem ser aproximadas por uma distribuição log-normal com parâmetros $$\mu = 7.2$$ e $$\sigma = 2$$.

Podemos simular as abundâncias esperadas para as espécies sorteando 200 números de uma log-normal com estes parâmetros:

     ab.comun <- rlnorm(n=200, meanlog=7.2, sdlog=2)

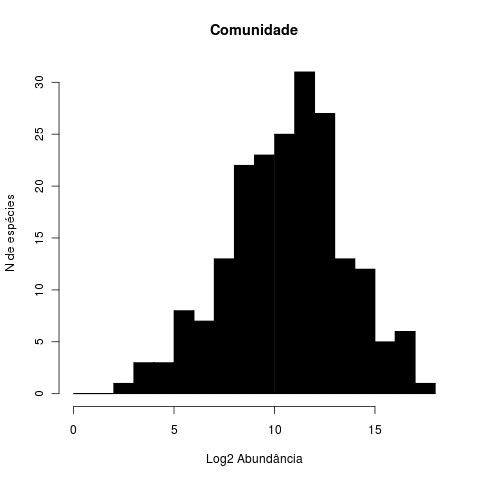
E geramos um histograma deste valores, em escala de log base 2 ¹⁾ com o comando:

hist(log(ab.comun,base=2),breaks=0:18, xlab="Log2 Abundância", 
     ylab="N de espécies", col="black", main="Comunidade")

Se tomamos uma amostra de uma certa fração do total de indivíduos da comunidade, a abundância esperada de cada espécie será sua abundância na comunidade multiplicada pela fração amostrada. Se uma espécie tem 200 indivíduos na comunidade, é esperado que sua abundância numa amostra de 1% da comunidade seja 2, e assim por diante.

Portanto, para calcular estes valores esperados para cada espécie numa amostra de 1% da comunidade, multiplicamos cada abundância por 0.01:

      ab.exp <- ab.comun*0.01

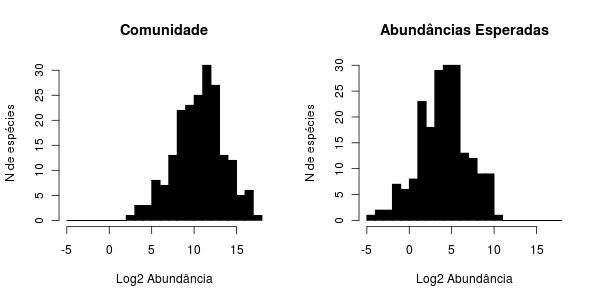
Isto vai apenas deslocar o histograma de abundâncias para a esquerda:

Os valores das abundâncias não serão exatamente estes esperados devido a flutuações ao acaso na amostra. Assim, precisamos de uma distribuição de probabilidades que defina as probabilidades de termos $$x$$ indivíduos na amostra, dada a abundância esperada.

Se os indivíduos são amostrados independentemente, podemos representar esta flutuação como uma variável Poisson.

Um exemplo de processo Poisson seria o lançamento de uma parcela em uma área com plantas distribuídas ao acaso. O valor esperado de plantas na parcela é a densidade de plantas multiplicada pela área da parcela, mas há a possibilidade de ter mais ou menos plantas do que este valor, dependendo de onde a parcela caia. Veja um exemplo detalhado desta simulação aqui.

Assim, a distribuição Poisson atribui uma probabilidade a cada valor de abundância, dado apenas o valor esperado, que corresponde ao único parâmetro da Poisson, chamado $$\lambda$$. Por exemplo, se abundância esperada é 2, as probabilidades de ter de zero a 10 indivíduos desta espécie numa amostra Poisson serão:

> dpois(0:5,lambda=2)
[1] 0.13533528 0.27067057 0.27067057 0.18044704 
[2] 0.09022352 0.03608941

Para simular uma amostragem Poisson de nossa comunidade com 200 espécies, sorteamos 200 números de uma Poisson, sendo que o parâmetro $$\lambda$$ para cada sorteio corresponde ao valor de abundância esperada:

     ab.sample.p <- rpois(n=200,lambda=ab.exp)

Neste sorteio podem haver zeros, que representam as espécies não incluídas na amostra. Como estas não são conhecidas pela amostragem, retiramos os zeros com:

     ab.sample.p <- ab.sample.p[ab.sample.p>0]

Há muitos casos em que os indivíduos estão agregados por unidade amostral, inclusive no caso de parcelas lançadas para amostrar comunidades vegetais. Neste caso, a Poisson não é um modelo adequado de amostragem, pois presume que as ocorrências dos indivíduos na amostra sejam independentes, o que corresponde a uma distribuição ao acaso no espaço.

A distribuição binomial negativa é muito usada para descrever amostras com agregação. Ela pode ser definida por uma parâmetro que corresponde ao valor esperado, e outro, que regula a intensidade de agregação, e pode ser interpretado como um índice de agregação.

As probabilidades de termos zero a cinco indivíduos em uma amostra binomial negativa com valor esperado de dois, e índice de dispersão de 0,1 ²⁾ são:

> dnbinom(0:5,mu=2,size=0.1)
[1] 0.73752725 0.07024069 0.03679274 0.02452850 
[5] 0.01810437 0.01413865

Comparadas com a Poisson para o mesmo valor esperado, amostras com pelo menos um indivíduo são bem menos prováveis. Para entender melhor porque, veja aqui.

Para simular uma amostragem com agregação de nossa comunidade com 200 espécies, sorteamos 200 números de uma Binomial Negativa, sendo que o parâmetro $$\mu$$ para cada sorteio corresponde ao valor de abundância esperada, e o índice de dispersão baixo (0,1):

     ab.sample.nb <- rnbinom(n=200,mu=ab.exp,size=0.1)

Novamente, retiramos os valores zero da amostra, pois são “invisíveis” para quem está amostrando:

     ab.sample.nb <- ab.sample.nb[ab.sample.nb>0]

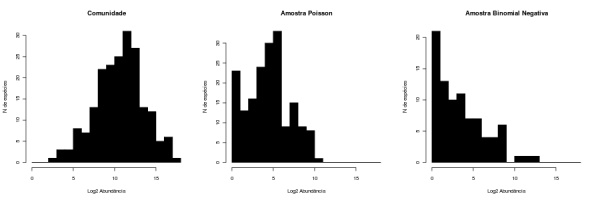
Agora podemos comparar as distribuições de abundâncias das duas amostras simuladas com a da comunidade, com histogramas:

par(mfrow=c(1,3))
hist(log(ab.comun,base=2),breaks=0:18, xlab="Log2 Abundância", 
     ylab="N de espécies", col="black", main="Comunidade")
hist(log(ab.sample.p,base=2),breaks=0:18, xlab="Log2 Abundância", 
     ylab="N de espécies", col="black", main="Amostra Poisson")
hist(log(ab.sample.nb,base=2),breaks=0:18, xlab="Log2 Abundância", 
     ylab="N de espécies", col="black", main="Amostra Binomial Negativa")
par(mfrow=c(1,1))

Com estas simulações mostramos que as distribuições de abundâncias que observamos não são as mesmas que as das comunidades, pois elas provêm de amostras. Experimente repetir as simulações variando número de espécies, a SAD da comunidade, proporção da comunidade amostrada e intensidade de agregação, para investigar o impacto de cada um destes fatores.

A mensagem geral é que para inferir sobre as SADs nas comunidades, temos que incluir em nossos modelos os processos amostrais. Isto foi feito por Fisher et al. (1943) para deduzir a distribuição de série logarítmica, e por Preston (1948) para propor a idéia da “linha de véu” da log-normal em uma amostra. Pielou (1977) e Green & Plotkin (2007) formalizaram este procedimento. Um resumo das deduções destes autores está aqui, e em Prado (2009, pdf abaixo).

<bibtex> @ARTICLE{,

author = {Fisher, R.A. and Corbet, A.S. and Williams, C.B.},
title = {The relation between the number of the species and the number of
individuals in a random sample from animal population},
journal = {Journal of Animal Ecology},
year = {1943},
volume = {12},
pages = {42-58},
owner = {paulo},
timestamp = {2009.04.12}

}

@ARTICLE{Green2007,

author = {Jessica L. Green and Joshua B. Plotkin},
title = {A statistical theory for sampling species abundances},
journal = {Ecology Letters},
year = {2007},
volume = {10},
pages = {1037 - 1045},
owner = {paulo},
timestamp = {2008.12.16},
url={http://www3.interscience.wiley.com/journal/118545784/suppinfo}

}

@BOOK{Pielou1977,

title = {Mathematical Ecology},
publisher = {John Wiley and Sons},
year = {1977},
author = {Pielou, E. C.},
address = {New York},
owner = {paulo},
timestamp = {2008.12.20}

}

@article{Preston1948,

title={The commonness, and rarity, of species},
author={Preston, FW},
journal={Ecology},
pages={254--283},
year={1948},
publisher={Duke University Press},
}

@ARTICLE{Prado2010,

author = {Prado, P I},
title = {Distribuições de Abundâncias de Espécies: avanços analíticos para entender um padrão básico em ecologia},
journal = {Ciência e Ambiente},
year = {2010},
volume = {no prelo},
file={:projetos:prado_2010.pdf}

}

</bibtex>