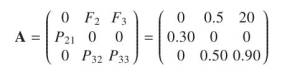Modelos Matriciais
Matriz de Leslie/Leftkovicth
 O crescimento de uma população com estrutura etária pode ser projetado utilizando-se álgebra matricial. As matrizes de Leslie contêm informação sobre as taxas de natalidade e mortalidade de diferentes classes etárias de uma população e são uma forma robusta de calcular o crescimento populacional e fazer projeções da população para diferentes cenários. Uma generalização da matriz de Leslie ocorre quando a população é classificada por estádios de desenvolvimento, e não por idade (matriz de Leftkovicth). Neste caso, um indivíduo de uma dada classe pode, além de morrer, crescer e reproduzir, permanecer no mesmo estádio a cada intervalo de tempo. Nessa generalização, as taxas vitais básicas (crescimento, sobrevivência e reprodução) estão embutidas nos valores das matrizes de transição, onde computamos o efeito que o número de indivíduos em cada classe estado exerce nas outras no intervalo de tempo seguinte.
O crescimento de uma população com estrutura etária pode ser projetado utilizando-se álgebra matricial. As matrizes de Leslie contêm informação sobre as taxas de natalidade e mortalidade de diferentes classes etárias de uma população e são uma forma robusta de calcular o crescimento populacional e fazer projeções da população para diferentes cenários. Uma generalização da matriz de Leslie ocorre quando a população é classificada por estádios de desenvolvimento, e não por idade (matriz de Leftkovicth). Neste caso, um indivíduo de uma dada classe pode, além de morrer, crescer e reproduzir, permanecer no mesmo estádio a cada intervalo de tempo. Nessa generalização, as taxas vitais básicas (crescimento, sobrevivência e reprodução) estão embutidas nos valores das matrizes de transição, onde computamos o efeito que o número de indivíduos em cada classe estado exerce nas outras no intervalo de tempo seguinte.
Objetivo
O objetivo desse exercício é entender como podemos tratar populações estruturadas com estes modelos matriciais.
Vamos começar com multiplicação de matrizes e análises de autovalor e autovetor!
Entrando na matriz...
 Vamos imaginar que coletamos em campo dados de uma população de palmeiras. Encontramos que a população é estruturada nos estágios: semente (F1), juvenil (F2) e adulto (F3). Imagine que 50% dos jovens sobreviveram e tornaram-se adultos, 90% dos adultos sobreviveram e que a cada 100 sementes encontradas, foram encontrados 30 juvenis. Ainda, estimamos a produção de sementes por indivíduos juvenis em 0,5 e por adultos em 20. Ou seja:
Vamos imaginar que coletamos em campo dados de uma população de palmeiras. Encontramos que a população é estruturada nos estágios: semente (F1), juvenil (F2) e adulto (F3). Imagine que 50% dos jovens sobreviveram e tornaram-se adultos, 90% dos adultos sobreviveram e que a cada 100 sementes encontradas, foram encontrados 30 juvenis. Ainda, estimamos a produção de sementes por indivíduos juvenis em 0,5 e por adultos em 20. Ou seja:
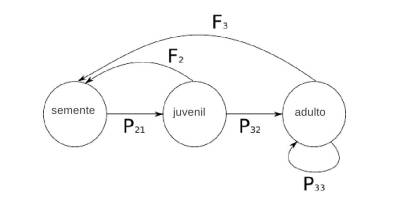
A partir dos dados obtidos podemos construir a nossa matriz de Leslie para a população em questão.
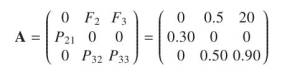
Num censo de número de indivíduos do sistema de estudo encontramos: 100 sementes, 250 juvenis e 50 adultos. O que nos dá um vetor de N(t) na condição inicial.
Vamos então fazer as projeções para esta população. No R, quando queremos fazer operações matriciais temos uma notação específica, para multiplicação de matriz, por exemplo usamos a notação %*%. E pronto! Ele faz a operação conforme as regrinhas matemáticas para isso.
# matriz de leslie
A <- matrix(c(0, 0.5, 20, 0.3, 0, 0, 0, 0.5, 0.9), nr = 3, byrow = TRUE)
A
# vetor de N iniciais da populacao
N0 <- matrix(c(100, 250, 50), ncol = 1)
Para fazermos a projeção da população para o tempo (em anos) seguinte:
$ N(t+1) = An(t) $
N1 <- A %*% N0
N1
Agora podemos projetar para um intervalo de tempo maior e ver o que acontece.
anos <- 10
N.projecoes <- matrix(0, nrow = nrow(A), ncol = anos+1)
N.projecoes[, 1] <- N0
for (i in 1:anos)
{
N.projecoes[, i + 1] <- A %*% N.projecoes[,i]
}
par(mfrow=c(1,2))
matplot(0:anos, t(N.projecoes), type = "l", lty = 1:3, ylab = "n(t)", xlab = "Tempo (t)", xlim=)
legend("topleft", legend = c("Sementes", "Juvenil", "Adulto"),lty = 1:3, col = 1:3, bty = "n")
matplot(0:anos, log(t(N.projecoes)), type = "l", lty = 1:3, ylab = "n(t)", xlab = "Tempo (t)", xlim=)
legend("topleft", legend = c("Sementes", "Juvenil", "Adulto"),lty = 1:3, col = 1:3, bty = "n")
<box 70% red | Exercício 1: Interpretando os gráficos >
</box>
Uma ajuda
Abaixo uma tem uma função para projetar populações a partir da matriz de transição e do estado inicial (tmax é o tempo máximo de projeção). É basicamente o que fizemos anteriormente, mas agora com a ajuda da função.
<box blue 90% | Função proj.mat>
########################
## Projeção Matricial
########################
proj.mat<-function(n0, matproj, tmax)
{
res.mat<-matrix(NA,nrow=tmax+1,ncol=length(n0))
res.mat[1,]<-n0
for(i in 2:(tmax+1))
{
res.mat[i,]=matproj %*% res.mat[(i-1),]
}
return(res.mat)
}
######################
## rodando a função ##
######################
nEst<-proj.mat(n0=N0, matproj=A , tmax=10)
matplot(1:11, nEst, type="l")
#########################
# tamanho da população ##
########################
nPop<-apply(nEst,1, sum)
plot(1:11, nPop)
</box>
Taxa de Crescimento
$ \lambda = \frac{N_{t}}{N_{t-1}}$
Vamos ver como a taxa de crescimento se comporta!
#############################
# Crescimento da População ##
#############################
lambPop<-nPop[2:11]/nPop[1:10]
matplot(1:10, lambPop, type="b", pch=1)
<box 70% red| Exercício>
OK! Agora vamos fazer um exercício!
projete a população a tempos mais longos!
veja como se comporta a taxa de crescimento da população $\lambda= \frac{N_t}{N_{t-1}}$
faça o mesmo variando algum parâmetro da matriz de transição
como se comporta essa taxa ao longo do tempo? Ele muda (qualitativamente) quando muda algum parâmetro da população (transições, estado inicial)?
</box>
Distribuição de Estádios
Uma característica importante da população é a distribuição relativa dos estádios em relação ao total de indivíduos da população. Será que a importância (proporção de indivíduos) de um estágio pode variar ao longo da trajetória da população? Vamos ver?!
##########################
# proporção das classes ##
##########################
propEst<-nEst/nPop
matplot(1:11, propEst, type="l")
<box 80% red | Exercício>
1. Qual a contribuição, em proporção de indivíduos, de cada classe (estágio) para o tamanho total da população a cada tempo?
2. Essa contribuição das classes varia ao longo do tempo?
3. Ilustre sua resposta com projeções de populações e gráficos dessas simulações.
4. Calcule a taxa de crescimento da população a cada intervalo de tempo e faça o gráfico dessa taxa ao longo do tempo.
</box>
<box 70% red| Exercício (de novo?!!)>
De novo, aumente o tempo da simulação para ver o que acontece
modifique os parâmetros da matriz de transição e do estado inicial para ver se a trajetória se modifica e quais as semelhanças qualitativas do comportamento.
</box>
Análise de Perturbação
Podemo inferir a contribuição de cada elemento da matriz de transição para a composição da taxa de crescimento populacional através de análises de perturbação da matriz.
A lógica é bastante intuitiva: se modificarmos uma das transições, mantendo todos os outros elementos da matriz constante, a variação no $\lambda$ será um reflexo da variação do elemento que modificamos. Desse modo, podemos analisar a contribuição de cada transição e consequentemente das taxas vitais em cada estádio para o crescimento da população. Na matriz do nosso exemplo a transição (no caso permanência) na fase de adulto é correspondente à taxa vital de sobrevivência nesse estádio. Podemos então fazer a seguinte pergunta:
Vamos responder essa pergunta?
###########################################
## Perturbando a sobrevivência do adulto ##
###########################################
pert=seq(0,1, by=.05)
resAd=rep(NA, length(pert))
names(resAd)<-paste("p", pert, sep="_")
for(i in 1:length(resAd))
{
Ai<-A
Ai[3,3]<-pert[i]
projAi= proj.mat(n0=N0,matproj=Ai, tmax=100)
nAi=apply(projAi, 1, sum)
lambi=nAi[101]/nAi[100]
resAd[i]<-lambi
}
resAd
<box 80% red| Exercício>
1. A sobrevivência do adulto tem muita influência no destino da população?
2. Se você fosse pensar em uma extração sustentável dessa população, como você poderia usar esta análise para fazer alguma recomendação para o manejo?
3. A extinção da população é imediata quanto a taxa de sobrevivência de adultos é zero?
4. Faça o mesmo para a transição de sementes para juvenil e compare com a sobrevivência do adulto. Qual transição é mais importante para o destino da população?
5. A proporção dos estádios em relação ao total da população é diferente entre cenários da matriz com perturbação e da matriz original?
</box>
Incluindo Denso-dependência
A análise de matrizes e a projeção da população permite grande flexibilidade para simular cenários nas populações. Podemos, por exemplo, incluir efeito de densidade em uma dos estágios na população e o efeito inverso em outro (denso dependência positiva ou negativa) ou mesmo incluir diminuição na sobrevivência e aumento na natalidade em um estágio.
Vamos aqui incluir o efeito de densidade na probabilidade de permanência da classe adulta.
Vamos usar uma equação em que o $P_{33} $ a permanência na classe adulta seja uma fração de da transição quando o N=0. Uma possibilidade é a função:
$$ P_{33} = P'_{33} * \frac{h}{h+N_3}$$
O que essa função significa? Vamos apenas verificar o que acontece com a expressão $\frac{h}{h+N_3}$
des<-function(n,h){h/(h+n)}
des.mat<-outer(seq(1,10,by=0.1), seq(1,10,by=0.1), des)
filled.contour(x=seq(1,10,by=0.1),y=seq(1,10,by=0.1),des.mat, color = terrain.colors, xlab="N", ylab="h", main="Proporção da taxa máxima")
<box 70% red | Exercício>
</box>
Mundo Real
 Vamos trabalhar agora com dados 1) de uma população de cactus (Coryphantha robbinsorum) ameaçada de extinção que ocorre em afloramentos calcários no Arizona e cercanias no México.
Seus estádios de vida foram definidos de forma similar ao exemplo anterior: juvenis pequenos, juvenis grandes e adultos, sendo que apenas o adulto se reproduz.
Vamos trabalhar agora com dados 1) de uma população de cactus (Coryphantha robbinsorum) ameaçada de extinção que ocorre em afloramentos calcários no Arizona e cercanias no México.
Seus estádios de vida foram definidos de forma similar ao exemplo anterior: juvenis pequenos, juvenis grandes e adultos, sendo que apenas o adulto se reproduz.
##################
### Matriz cory ##
##################
cory<-matrix(c(0.434, 0.333,0,0,0.61, 0.304,0.56, 0, 0.956), ncol=3, nrow=3)
cory
A função a seguir opera diretamente a matriz de transição para incorporar a denso dependencia. Veja como a população de cory se comporta!
ddf<-function(n, mat, h, st)
{
mat[st, st]<-mat[st,st]*(h/(h+n[st]))
return(mat)
}
cory
# estado inical
n0=matrix(c(10,5,2), ncol=1)
## tempo 1
n1 = cory %*% n0
n1
n1d= ddf(n0,cory,h=10, st=3)%*% n0
n1
n1d
## tempo 2
n2 = cory %*% n1
n2
n2d= ddf(n1,cory,h=10, st=3)%*% n1
n2
n2d
## tempo 3
n3 = cory %*% n2
n3
n3d= ddf(n2,cory,h=10, st=3)%*% n1
n2
n2d
Vamos incluir essa função em uma outra para podermos fazer projeções para qualquer tempo:
############################
## função:denso-dependência
###########################
proj.dd<-function(n0, matproj,h, st, tmax=10)
{
res.mat<-matrix(NA,nrow=tmax+1,ncol=length(n0))
res.mat[1,]<-n0
for(i in 2:(tmax+1))
{
res.mat[i,]=ddf(res.mat[(i-1),], matproj,h, st) %*% res.mat[(i-1),]
}
return(res.mat)
}
## tmax = 20
res.corydd<-proj.dd(n0,matproj=cory, h=100, st=3, tmax=20)
res.corydd
matplot(0:20,res.corydd, type="l")
prop.estdd<-res.corydd/apply(res.corydd,1,sum)
matplot(0:20,prop.estdd, type="l", lty=2:4, col=2:4)
## tmax = 100
res.corydd<-proj.dd(n0,matproj=cory, h=100, st=3, tmax=100)
res.corydd
matplot(0:100,res.corydd, type="l", ylab="N")
prop.estdd<-res.corydd/apply(res.corydd,1,sum)
matplot(0:100,prop.estdd, type="l", lty=2:4, col=2:4, ylab="Proporção das classes")
<box 80% red| Exercício>
1. aumente o tempo (tmax=100) de projeção para o exemplo acima e compare com uma população sem denso-dependência. Apresente os gráficos!
2. diminua e depois aumente o h e veja qual o efeito na trajetória da população
3. o estado inicial da população influencia a projeção quanto ao estado final da população? Há alguma similaridade com relação ao modelo sem densidade-dependência?
</box>
Autovalores e autovetores
Análise de autovalores e autovetores é uma transformação linear de matrizes para sumarizar dados multivariados. De maneira que:
$ Aw = \lambda w $
onde A é a matriz, w é o autovetor, e $ \lambda $ é o autovalor.
Hein? Veja este linque para uma explicação melhor.
O que acontece é que frequentemente em Ecologia ouvimos dizer de autovalores e autovetores. Isso aparece em: em análises multivariadas de ordenação; análises de estabilidade com uma ou mais espécies e em análises de matrizes projeção populacional!
Para o nosso caso em crescimento populacional estruturado podemos encontrar o $\lambda$ assintótico simplesmente encontrando o autovalor dominante da matriz de projeção. Autovalores são representados por $ \lambda $ e correspondem à solução para a equação acima. O autovalor dominante é aquele com o maior valor absoluto e geralmente é um número complexo. Em matrizes de projeção, o $ \lambda_{1} $ é sempre positivo e real. Podemos usar análises de autovalor e autovetor para encontrar o $ \lambda_{1} $ como se fosse mágica. Para fazermos operações com números complexos no R usaremos a função Re.
<box 80% green |Resumindo>
O autovalor dominante de uma solução matricial é um valor escalar 2) que é equivalente 3) à matriz ao multiplicar um vetor.
Em outras palavras é a nossa taxa assintótica de crescimento: o $ \lambda $.
</box>
Para entender isso, vamos refazer o gráfico do crescimento assintótico da população!
res.cory<-proj.mat(n0,matproj=cory, tmax=100)
res.cory
matplot(0:10,res.cory[1:11,], type="l")
prop.est<-res.cory/apply(res.cory,1,sum)
matplot(0:100,prop.est, type="l", lty=2:4, col=2:4)
matplot(0:10,prop.est[1:11,], type="l", lty=2:4, col=2:4)
legend("topleft", lty=2:4, col=2:4, legend=c("small", "large","adults"))
lamb.seq=res.cory[2:101]/res.cory[1:100]
plot(1:100, lamb.seq,type="l", lty=2)
Agora vamos calcular o autovalor da matriz e comparar com a taxa assintótica de crescimento.
eigen.cory=eigen(cory)
lamb=max(Re(eigen.cory$values))
lamb
abline(h=lamb,col="red")
Ou seja, uma maneira de achar o lambda (mais intuitiva para nós na Ecologia) é iterar o crescimento populacional por um longo período de tempo, com o aumento de t a taxa de crescimento anual R(t) se aproxima a $ \lambda_{1} $. Outro modo mais direto é através do autovalor dominante da matriz de transição!
Distribuição de Estágios Estável
A abundância relativa dos diferentes estágios de vida é chamada de distribuição de estágios. Para uma população estruturada na qual as taxas demográficas são constantes a estrutura de estágios irá atingir uma distribuição de estágios estável. A população pode crescer (como esperado pelo crescimento exponencial), mas as abundâncias relativas em cada estágio permanece constante. E já vimos isso antes…
Então, voltando aos autovalores e autovetores podemos encontrar a distribuição de estágios estável. Agora o que nos dará a abundância relativa será o autovetor dominante, w. O autovetor dominante está na mesma posição do autovalor dominante. Podemos então extrair o w, mantendo sua parte real e dividir pela sua soma.
Voltando então à nossa matriz “A” com os dados hipotéticos de uma população de palmeiras.
aval.A <- eigen(A)
w <- Re(aval.A$vectors[,1]) # indexamos pela posicao 1 que eh a posicao correspondente do autovalor dominante
w
round(w/sum(w), 3)
<box 70% red | Exercício>
Agora volte para a nossa projeção de N(t) (baseada na nossa matriz A) e calcule a partir de que ano a proporção de indivíduos em cada classe se ajusta à distribuição de estágios estável obtida acima. Lembre que os valores estão guardados na matriz N.projecoes.
</box>
# voltando
matplot(0:anos, log(t(N.projecoes)), type = "l", lty = 1:3, ylab = "n(t)", xlab = "Tempo (t)", xlim=)
legend("topleft", legend = c("Sementes", "Juvenil", "Adulto"),lty = 1:3, col = 1:3, bty = "n")
# lembrando que:
colnames(N.projecoes) <- paste("N", 0:10, sep="")
rownames(N.projecoes) <- c("semente","juvenil", "adulto")
N.projecoes
Valor reprodutivo
A estrutura de estágios estável nos dá uma medida da importância do estágio (em termos de abundância relativa) no crescimento estruturado. No caso do valor reprodutivo temos uma medida da importância do indivíduo em cada estágio, ou seja, o valor reprodutivo é a contribuição esperada de cada indivíduo na reprodução presente e futura. Caracterizamos todos os indivíduos em um estado com o mesmo valor reprodutivo. Usando álgebra linear, encontramos o valor reprodutivo resolvendo:
$ vA = \lambda v $
$ VR = \frac{\nu_1}{\sum^{S}_{i=1}{\nu_1}} $
Podemos obter o autovalor esquerdo realizando uma análise de autovalor na matriz de projeção transposta. As posições do autovalor dominante direito e esquerdo são as mesmas. Extraímos apenas o autovetor esquerdo e o escalonamos, de maneira que o valor reprodutivo do primeiro estágio é 1.
De novo com a nossa matriz “A”.
M <- eigen(t(A))
M
v <- Re(M$vectors[, which.max(Re(M$values))])
VR <- v/v[1]
VR
<box 70% red | Exercício >
Como você interpretaria o aumento dos valores reprodutivos encontrados?
</box>
Sensibilidade e elasticidade
Sensibilidade e elastividade referem-se à importância relativa de cada transição (i.e. cada seta no diagrama de ciclo de vida, ou cada elemento na matriz de Leslie) na determinação do $ \lambda $. Ambas combinam informações de estrutura de estágio estável e dos valores reprodutivos.
Sensibilidade: representa a contribuição direta de cada transição no $ \lambda $. Em termos matemáticos seria: sensibilidade dos elementos $a_{ij}$ da matriz de projeção A corresponde às mudanças no $ \lambda $, dadas a mudanças em cada elemento ($ \frac{\delta \lambda}{\delta a_{ij}}$). E é calculada como:
$ \frac{\delta \lambda}{\delta a_{ij}} = \frac{\nu_{ij} \omega_{ij}}{vw}$
vw.s <- v %*% t(w)
(S <- vw.s/as.numeric(v %*% w))
Elasticidade: é a sensibilidade ponderada pelas probabilidades de transição. Corresponde ao ajuste das sensibilidades de maneira a levar em conta as magnitudes relativas dos elementos de transição, o que gera a elasticidade $e_{ij}$, onde:
$ e_{ij} = \frac{a_{ij} \delta \lambda}{\lambda \delta a_{ij}}$
L1 <- Re(aval.A$values[1])
elas <- (A/L1) * S
round(elas, 3)
Parece complicado?!
No entanto você já fez isso e entendeu tudo! Quando fizemos o roteiro de perturbação da matriz, calculamos a contribuição de um componente da matriz de transição (a sobrevivência dos adultos) na variação do lambda. A sensibilidade é a mesma coisa… só que, derivada diretamente da matriz de transição.
A elasticidade é a sensibilidade proporcional ao efeito. Ou seja, uma transição com valor muito pequeno pode duplicar e isso ter uma efeito pequeno no lambda, enquanto outra ao duplicar tem um efeito muito mais pronunciado, independente da dimensão dessas transições!
Comparando as análises
Vamos agora fazer uma sequência de análises usando a álgebra matricial e depois compará-la com o pacote popbio do R para análises matriciais de dinâmica populacional!
E para finalizar, faremos os cálculos com o nosso modelo para o cacto.
####################
### EigenAnalise ####
####################
plot(1:100, lamb.seq, xlab="lambda", ylab="times", cex=0.7)
eigen.cory=eigen(cory)
eigen.tcory=eigen(t(cory))
lamb=max(Re(eigen.cory$values)) # calculo lambda1 confere
lamb
abline(h=lamb,col="red")
v.cory=Re(eigen.cory$vectors[,which.max(Re(eigen.cory$values))]) # calculo de valor proporcional ao valor reprodutivo ok!
v.cory
vr.cory=v.cory/v.cory[1]
vr.cory # agora sim o valor reprodutivo padronizado para escala da primeira classe
w.cory=Re(eigen.tcory$vectors[,which.max(Re(eigen.tcory$values))])#stage stable vector ok!
w.cory/sum(w.cory)
prop.est[100,]
### sensibilidade
vms.cory=vr.cory%*%t(w.cory)
S.cory=vms.cory/as.numeric(vr.cory%*%w.cory) ## Funciona!!! Só precisa substituir por zero transicoes não existentes...pois ele calcula
### elasticidade
(cory/lamb)*S.cory
##############################
## conferindo nossos cálculos
#############################
# se voce ainda nao tem o pacote popbio, instale-o com o comando abaixo retirando a #:
# install.packages("popbio")
library(popbio)
eigen.analysis(cory)