Para as funções que diferenciamos na mão durante a aula, (1) confira o resultado no Maxima,(2) produza um gráficos lado a lado da função e sua derivada, no intervalo definido.
intervalo: -1 a +1
intervalo: -10 a +10
intervalo: -1 a +1
intervalo: -10 a +10
intervalo: -100 a +100
intervalo: 0 a +2
intervalo: -50 a +50
intervalo: -1 a +1
intervalo: -1 a +1
intervalo: -1 a +1
intervalo: 1 a +20
<box 80% green |Dicas>
Veja um exemplo de código abaixo:
############
# 1. f(x)=5x^2+4
############
par (mfrow=c(1,2))
f1=function(x){5*x^2 +4}
curve(f1,-1,+1)
## derivada
df1=function(x){10*x}
curve(df1,-1,+1)
############
</box>
 A baleia-bicuda-de-cuvier (Ziphius cavirostris) parece ter sua área de alimentação associada a inclinação e profundidade do assoalho marinho. Para estudar essas baleias um pesquisador hipotético 1) definiu um transecto de 5 Km (Oeste → Leste), a partir da costa, onde estudou o comportamento da Baleia.
A baleia-bicuda-de-cuvier (Ziphius cavirostris) parece ter sua área de alimentação associada a inclinação e profundidade do assoalho marinho. Para estudar essas baleias um pesquisador hipotético 1) definiu um transecto de 5 Km (Oeste → Leste), a partir da costa, onde estudou o comportamento da Baleia.
Os dados de profundidade foram medidos nas seguintes distâncias (Km) do transecto:
dist=c(0,0.5, 1, 1.35, 1.72, 2.05,2.4, 3, 3.3, 3.77, 4, 4.5, 5 )
prof=c(-0.1, -0.5, -0.98, -1.12, -1.4, -.95, -1.05, -1.9, -2.33, -2.88, -2.85, -2.1, -2.2)
Para definir um modelo de profundidade o pesquisador usou uma expressão polinomial de sexto grau:
mod.prof<-lm(prof~dist + I(dist^2) + I(dist^3) + I(dist^4) + I(dist^5) + I(dist^6))
O gráfico abaixo representa os dados e o modelo ajustado a eles:
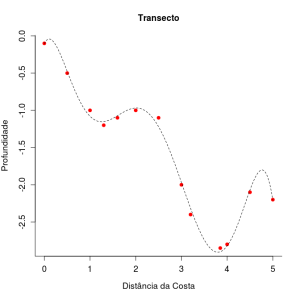
dist=c(0,0.5, 1, 1.35, 1.72, 2.05,2.4, 3, 3.3, 3.77, 4, 4.5, 5 )
prof=c(-0.1, -0.5, -0.98, -1.12, -1.4, -.95, -1.05, -1.9, -2.33, -2.88, -2.85, -2.1, -2.2)
plot(prof~dist)
mod.prof<-lm(prof~dist + I(dist^2) + I(dist^3) + I(dist^4) + I(dist^5) + I(dist^6))
mod.prof$coefficients
plot(prof~dist,main="Transecto", ylab="Profundidade", xlab="Distância da Costa", pch=19, col="red", cex.axis=1.2, cex.lab=1.2, bty="l")
xdist=seq(0,5, by=0.001)
lines(xdist, predict(mod.prof,newdata=data.frame(dist=xdist)), type="l", lty=2)
savePlot(file="grafTrans.png", type="png")


