Modelos Densidade Independente
Em uma população onde as taxas de nascimento e mortalidade são constantes (não são afetadas pelo tamanho da população), dizemos que essa população tem um crescimento independente da densidade dela própria.
Essa situação é geralmente relacionada a uma ausência de restrição ao crescimento, onde os recursos são ilimitados, mas pode também estar associada a uma depleção de recursos e à extinção da população.
Taxa de crescimento
Vamos imaginar agora uma população hipotética com taxas constante de crescimento e mortalidade e sem migrações. A cada ciclo de tempo relacionado a uma geração (T), o tamanho da população é o resultado do número de indivíduos da geração anterior mais números de nascimentos (B), menos mortes (D).
$$N_{T+1} = N_T + B - D $$
Podemos relacionar o número de mortes e nascimentos a um valor per capita:
onde: b = taxa de nascimento per capita a cada geração ; d = taxa de mortalidade per capita a cada geração.
Note que a taxa não muda com o tamanho da população, entretanto, o número de nascimentos e mortes é proporcional ao tamanho populacional. Vamos apenas deixar claro mais uma premissa, para fins didáticos: os nascimentos e mortalidades ocorrem simultaneamente na população (p.ex: uma planta anual).
Sendo T a escala de uma geração, podemos então dizer que :
se: $r_T = b-d$ ; fator de crescimento discreto
Como $ 1+r_T $ é uma constante, vamos designá-la como $\lambda$, um número positivo que mede o aumento proporcional da população de uma geração a outra. Portanto:
$$ N_{T+1} = \lambda N_T$$
Projetando a População
Podemos então projetar a nossa população a cada ciclo de tempo (gerações). Por exemplo:
Se uma população com 100 indivíduos tem uma taxa per capita de natalidade de 0,8/ano e de mortalidade de 0,75/ano, qual o tamanho esperado da população no próximo ano?
N0=100
lamb=1+(0.8-0.75)
Nt1=N0*lamb
Nt1
Podemos também projetar a população para outras gerações, usando iterações:
(Nt2=Nt1*lamb)
(Nt3=Nt2*lamb)
(Nt4=Nt3*lamb)
Note que:
Essa equação recursiva pode ser escrita como:
$$N_{T}=\lambda^T N_0 $$
Vamos pegar nosso exemplo anterior e projetá-lo para 10 ciclos de tempo.
N0=100
lamb=1+(0.8-0.75)
tmax=10
tseq=0:tmax
Nseq=N0*lamb^tseq
Nseq
plot(tseq, Nseq, type="l")
Tamanho Inicial
Vamos agora explorar o tamanho inicial da população.
$N_0 = 10,20,30, 40 $
$\lambda = 1,5$
$ tempo = 1:10$
tseq=0:10
lamb=1.5
N0=c(10,20,30,40)
N0.mat=matrix(N0, ncol=length(tseq), nrow=length(N0))
N0.mat
lamb_t=lamb^tseq
lambt_mat=matrix(lamb_t,ncol=length(tseq), nrow=length(N0), byrow=TRUE)
Nt=N0.mat*lambt_mat
colnames(Nt)<-paste("t", 0:10, sep="")
rownames(Nt)<-paste("N0", c(10,20,30,40), sep="_")
Nt
matplot(0:10,t(Nt))
Vamos agora colocar o mesmo gráfico em uma escala logarítmica para o eixo y.
par(mfrow=c(1,2))
matplot(0:10,t(Nt))
matplot(0:10, t(Nt), log="y")
O que está acontecendo?? Parece que todas as populações crescem igualmente quando estamos em uma escala logarítmica!
Vamos investigar a equação que estamos usando, $N_t=\lambda^T N_0$ e tirar o log dos dois lados da equação:
Essa equação lembra uma equação da reta $ y=ax+b $, onde o intercepto é $log(N_0)$ e a inclinação é iqual a $log{\lambda}$.
Desafio
 Vamos agora investigar os dados do tamanho populacional de uma espécie de pardal norte-americano (Melopiza melodia) partindo da premissa que essa população cresce em tempo discreto, já que os nascimentos ocorrem em um intervalo curto de tempo de nidificação a cada ano.
<box 320 green>
Vamos agora investigar os dados do tamanho populacional de uma espécie de pardal norte-americano (Melopiza melodia) partindo da premissa que essa população cresce em tempo discreto, já que os nascimentos ocorrem em um intervalo curto de tempo de nidificação a cada ano.
<box 320 green>
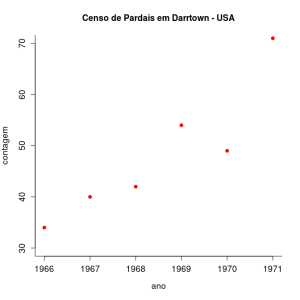
O gráfico representa a contagem de pardais cantores na cidade de Darrtown, OH, USA.
Baixe os dodos do arquivo pardal.txt no seu computador.
</box>
Vamos calcular os $\lambda$ para os cinco primeiros intervalos:
pardal<-read.table("pardal.txt", header=TRUE, sep="\t", as.is=TRUE)
str(pardal)
head(pardal)
pardal6= pardal[1:6,]
plot(pardal6$Count ~pardal6$Year)
lamb_pardal=pardal6$Count[2:6]/pardal6$Count[1:5]
lamb_pardal
Agora, vamos calcular a projeção da população pela média aritmética e geométrica dos $\lambda$ e desenhar as projeções junto com os dados observados!
#media aritmetica
(lamb.art = mean(lamb_pardal))
#media geometrica
(lamb.geo = prod(lamb_pardal)^(1/5))
tseq=0:5
plot(tseq, pardal6$Count, pch=19)
N0=pardal6$Count[1]
lines(tseq, N0*lamb.art^tseq, lty=2, col="red")
lines(tseq, N0*lamb.geo^tseq, lty=3, col="blue")
Crescimento Discreto
Abaixo tem o código de uma função base para a projeção do crescimento crescimento de uma população, que pode ser usada como estrutura básica para outras funções que iremos desenvolver no curso. No caso, é uma funcão com 3 argumentos: número de indivíduos no tempo 0 (N0), taxa de crescimento populacional (lamb) e o tempo máximo (tmax) de projeção da população.
cresc.geom= function(No=100, lamb=1.04, tmax=10)
{
resulta <- rep(NA,tmax)
resulta[1] <- No
for (i in 2:tmax)
{
tam=resulta[i-1]*lamb
resulta[i]=tam
}
return(resulta)
}
Ao copiar esse código na área de trabalho do R, um novo objeto é criado, de nome cresc.geom. Ele é um objeto da classe função que você pode usá-lo digitando o seu nome e especificando seus argumentos, como no exemplo a seguir:
resultado <- cresc.geom(No=10, lamb=0.98, tmax=100)
Note que o resultado da função, nesse caso, será guardado no objeto resultado. Para fazer um gráfico dos resultados pode utilizar o código abaixo:
plot(1:length(resultado), resultado)
Crescimento Contínuo
Nem todos os organismos são como plantas que tem uma época reprodutiva bem definida e que, em parte, podem ser modelados com o tempo discreto. Mesmo partindo da premissa que todos os nascimentos ocorrem em um curto intervalo de tempo anualmente (como no caso dos pardais), a mortalidade ocorre continuamente nessas populações. Para a grande maioria das populações nascimentos ocorrem praticamente a qualquer instante e são assincrônicas, o crescimento discreto não parece uma boa descrição desse fenômeno.
Vamos modelar uma população que tem uma taxa de crescimento anual de $\lambda = 1,5$.
Agora, vamos supor que essa mesma população tenha dois ciclos reprodutivos anuais, portanto temos que modelar seu crescimento por semestre, o que equivale a dizer que:
Ou seja, essa população tem uma taxa de crescimento de $\lambda = 1+ 0.25 $ por semestre. Trimestralmente teria uma taxa de (1 + 0.5/4)^4 e assim por diante, podemos então descrever:
$$ \frac{N_1}{N_0}= (1+\frac{r_d}{n})^n $$
O que acontece se deixarmos o número de frações de tempo cada vez maior, tendendo a um número infinitamente grande?
$$ \lim\limits_{\to \infty}(1+\frac{r_d}{n})^n$$
Vamos tentar resolver o limite acima de forma bruta, aumentando o número de divisões dentro de um ano da nossa taxa de crescimento discreta. A principio vamos deixar o $\lambda =2$, portanto o $r_d=1$ e o $N_0=1$ ; portanto $\frac{N_t}{N_0}= N_t$. Em seguida vamos fazer $\lambda =3$ e $\lambda =1.5$ (r=2 e r=0.5).
##############################
#### Crescimento Contínuo ####
##############################
n<- c(0:100, 200, 500,1000, 10000, 100000,1e+10)
N0 <- 1
rd1 <- 1
N1<-N0* (1+ rd1/n)^n
N1_N0= N1[length(N1)]/N0
plot(1:103, N1[1:103]/N0, type="l")
text(x=50, y=2.5, labels= paste("Máximo = ", N1[length(N1)/N0]))
N1_N0
exp(1)
rd2=2
N1a<-N0* (1+ rd2/n)^n
N1a_N0= N1a[length(N1a)]/N0
N1a_N0
exp(2)
rd.5=0.5
N1b<-N0* (1+ rd.5/n)^n
N1b_N0= N1b[length(N1b)]/N0
N1b_N0
exp(0.5)
Acima, demostramos na força bruta que:
$$ \lim\limits_{\to \infty}(1+\frac{r_d}{n})^n = e^r$$
Ou seja:
$$\frac{N_t}{N_0}=e^{rt} $$
$$N_t= N_0 e^{rt}$$
Chegamos a equação de crescimento contínuo!!
Além disso, chegamos a relação entre a taxa intrínseca de crescimento instantâneo e a taxa de crescimento discreto da população:
$$ \lambda = e^r $$ ou
$$ r = log_n(\lambda)$$
Equação diferencial
O mesmo problema do crescimento contínuo pode ser abordado de outra forma, utilizando uma equação diferencial.
Nesse caso, podemos dizer que a taxa de variação instantânea da população é igual a uma taxa intrínseca de crescimento (r), multiplicado pelo tamanho da população (N).
$$ \frac{dN}{dt}=rN $$
O  Maxima pode nos ajudar a solucionar a equação diferencial.
Digite as seguintes expressões, indicando que você quer resolver (ode2) a equação diferencial acima:
Maxima pode nos ajudar a solucionar a equação diferencial.
Digite as seguintes expressões, indicando que você quer resolver (ode2) a equação diferencial acima:
diff(N(t),t)=r*N(t);
ode2(%, N(t), t);
O resultado deve ser:
$ N(t)=c * e^{rt} $
Como o c representa o intercepto ou a situação inicial do sistema, o nosso $N_0$, chegamos novamente a:
$$ N_t= N_0 e^{rt} $$
Função Crescimento Exponencial
A partir da função cresc.geom, vamos criar uma função de crescimento contínuo exponencial. Há várias formas de fazê-la, mas vamos usar uma lógica que, apesar de não ser a mais eficiente 1), vai nos ajudar em outro passos de exercícios futuros.
Basicamente, temos que mudar:
tam=resulta[i-1]*lamb
muda para
tam=resulta[i-1]*exp(rc)
O resto permanece como estava:
cresc.exp= function(No=100, rc=0.04, tmax=10)
{
....
tam=resulta[i-1]*exp(rc)
....
}
Estocasticidade Ambiental
Flutuações ambientais podem exercer efeito na taxa de crescimento instantâneo da população. De uma forma simples, podemos imaginar que essa variação funcione como um ruído no r, como se a população em média tivesse uma taxa, mas a cada realização ela pudesse ser um tanto diferente devido a condições externar a ela própria. A implementação dessa estocasticidade ambiental em modelos contínuos é um pouco mais complicada, mas podemos imaginá-la como realizações em algum intervalo pequeno de tempo.
Para um crescimento discreto a construção de simulações com estocasticidade ambiental é mais intuitivo: a cada realização o Lambda é afetado pela variação ambiental. Vamos fazê-la.
npop=10
n0=10
lamb.med = 1.2
lamb.sd= 0.4
lamb = rnorm(npop, mean=lamb.med, sd=lamb.sd)
N0=rep(n0,npop)
N1=lamb*N0
lamb=rnorm(npop, mean=lamb.med, sd=lamb.sd)
N2=N1*lamb
N3=N2*rnorm(npop,mean=lamb.med,sd=lamb.sd)
N4=N3*rnorm(10,mean=lamb.med,sd=lamb.sd)
N5=N4*rnorm(10,mean=lamb.med,sd=lamb.sd)
Nt<-rbind(N0,N1,N2,N3,N4,N5)
matplot(0:5, Nt, type="l", lty=2:7)
Desafio
É possível adaptar a nossas função anterior de crescimento discreto para que possa também modelar populações com estocasticidade ambiental!
<box 70% green |Dicas>
O primeiro passo sempre e pensar quais argumentos vamos precisar
Nesse caso, temos apenas mais um argumento o lamb.dp : o desvio padrão de lambda. O resto continua o mesmo, lembre-se que se o lamb.dp for 0, nosso população é determinística! Ou seja, a mesma função pode se prestar para simular ambos cenários.
</box>


