Competição Interespecífica
Modelo em Tempo Discreto
O objetivo deste exercício é fazer uma projeção do tamanho populacional de duas populações competidoras, usando uma aproximação de modelos de Lotka-Volterra em tempo discreto.
Baixe a função a seguir e veja as sugestões de simulações no final do próprio código (não esqueça de tirar o símbolo “#” do inicio da linha para que o código seja lido no R)
<box 80% green | Competição>
Baixe o código da função de competição Lotka-Volterra em tempo discreto aqui. As legendas dos gráficos estão em inglês por se tratar de uma função que estamos preparando para um pacote oficial do R! Qualquer erro que encontrar nos avise.. estamos em fase de testes.
</box>
<box 70% red | Exercício 1: Aplicando a Função >
Teste a função com N01=10, N02=10, r1=0.05, r2=0.03, k1=80, k2=50, alfa=1.2, beta=0.5, e tempo final 200.
As isoclinas se cruzam? O que isso significa?
Teste a função com r1=0.05, r2=0.03, k1=80, k2=50, alfa=1.2, beta=0.5 e tempo final 50. Olhando as curvas de crescimento, você prediria que as espécies podem coexistir? E olhando as isoclinas, qual seria sua conclusão?
Experimente, para as duas combinações de parâmetros acima, usar tamanhos de populações iniciais diferentes. Isso faz alguma diferença? Discuta em termos de pontos de equilíbrio do modelo.
Busque um exemplo de combinação de k1, k2, alfa e beta que leve a cada um dos cenários possíveis no modelo:
espécie 1 vence a competição
espécie 2 vence a competição
coexistência em equilíbrio estável
exclusão com equilibrio instável (DICA: veja tabela 5.1 do Gotelli)
Dê uma interpretação biológica para as condições que levam a coexistência entre duas espécies.
</box>
Modelo Contínuo
Vamos usar novamente o pacote deSolve para aproximar a solução das equações de competição em tempo contínuo. Uma diferença importante é que, como agora temos 2 espécies, precisamos ter duas condições iniciais, e a função que vamos usar precisa retornar dois números.
Copie a função abaixo para o R:
cLVcomp=function(t,n,prts)
{
with(as.list(prts),{
dn1.dt= r1*n[1]*((k1-n[1]-alfa*n[2])/k1)
dn2.dt= r2*n[2]*((k2-n[2]-beta*n[1])/k2)
list(c(dn1.dt,dn2.dt))
})
}
Agora vamos estabelecer parâmetros e condição inicial para rodar o modelo e produzir o gráfico:
library(deSolve)
prmts<-c(r1=0.05,r2=0.03,k1=80,k2=50,alfa=1.2, beta=0.5)
N0<-c(10,10)
res=ode(y=N0, times=seq(1,100,0.01), func=cLVcomp, parms=prmts)
matplot(res[,1],res[,-1], type="l", ylab="Número de indivíduos", xlab="tempo", main="Modelo de Competição Lotka-Volterra")
Vamos agora aumentar o tempo de simulação:
res=ode(y=N0, times=seq(1,200,0.01), func=cLVcomp, parms=prmts)
matplot(res[,1],res[,-1], type="l", ylab="Número de indivíduos", xlab="tempo", main="Modelo de Competição Lotka-Volterra")
<box %70 red | Exercício 2: Usando o modelo contínuo >
- Copie o código acima e modifique os valores dos parâmetros para obter as situações de: (1) Coexistência estável; (2) Equilíbrio instável; (3) Extinção de cada uma das espécies.
- Use os parâmetros r1=0.5, r2=0.3, k1=80, k2=50, alfa=1.2, beta=0.5, e condições iniciais n01=100, n02=10. Encontre as soluções em tempo discreto e tempo contínuo com tmax = 200. Os gráficos parecem diferentes? Agora encontre as soluções para tmax=5. Qual é a diferença?
</box>
Mais espécies
<box %70 red | Exercício 3 >
- O que acontece se três espécies estiverem competindo entre si? Escreva as equações para um sistema com três competidoras, e interprete os parâmetros das equações.
</box>
Compete Maxima
O Prof. Paulo Inácio fez um roteiro muito simples para visualizar a trajetória de populações no modelo LV, usando o Maxima. A função plotdf cria um gráfico do campo de direção de uma Equação Diferencial Ordinária (EDO) de primeira ordem ou um sistema de duas EDO's de primeira ordem autônomas, de forma simples e direta. Isso é uma ferramenta bastante interessante para a visualização e interpretação dos modelos que estamos tratando nesse roteiro.
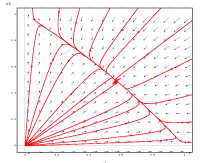
O uso do Maxima em sua interface gráfica (wxMaxima) é bastante intuitivo, como já vimos. No entanto, para desfrutar dos recursos que precisamos aqui há a necessidade, além do Maxima e sua interface gráfica de usuário padrão o wxMaxima, uma outra interface chamada xMaxima. Veja o site http://maxima.sourceforge.net/download.html para
instalação.
instale o xMaxima;
baixe o arquivo do roteiro do exercício
aqui abra o wxMaxima e abra o arquivo do roteiro;
quando abrir uma janela gráfica, experimente clicar com o mouse em algum ponto do gráfico;
LINDO! agora interprete o que está sendo mostrado!

O MAXIMA É O MÁXIM0!
<box 80% red| Exercício 4>
Uma outra forma de interpretar a capacidade de suporte de uma população é pensar nela como a influência que cada indivíduo da população exerce na taxa de crescimento intrínseco da população:
Nesse caso a equação logística para uma espécie ficaria:
$$\frac{dN_1}{dt} = r_1N_1(1- \alpha_{11} N) $$
Note que $\alpha_{11} = \frac{1}{K_1}$
qual a interpretação biológica de $\alpha_{11}$ ?
transforme as equações de Lotka-Volterra em tempo contínuo dadas em aulas para expressões que incorporem o equivalente a $\alpha_{11}$ e $\alpha_{22}$ para ambas espécie.
faça os gráficos do espaço de fase de duas espécies, usando os $\alpha_{11}$ e $\alpha_{22}$ ao invés de K1 e K2
modifique as funções da aula para conterem $\alpha_{21}$ e $\alpha_{12}$ (o beta da aula teórica) e verifique as situações de equilíbrio das populações dependendo do estado inicial em cada espaço do gráfico de fase. Utilize as quatro situações mostradas em aula relacionadas a capacidade competitiva de cada espécie (tabela 5.1 (b) do Gotelli), o equivalente a:
1.
2.
3.
4.
Note que a notação de $\alpha $ aqui corresponde a: primeiro número espécie afetada e segundo a espécie que afeta.
</box>


