Modelo Predador-Presa
 Uma companhia britânica que comercializava peles de lince Canadense desde o final do século XVIII, Hudson´s Bay Company, forneceu dados muito contundentes da interação predador-presa, relacionando o tamanho da população do lince com sua presa, uma lebre.
Uma companhia britânica que comercializava peles de lince Canadense desde o final do século XVIII, Hudson´s Bay Company, forneceu dados muito contundentes da interação predador-presa, relacionando o tamanho da população do lince com sua presa, uma lebre.
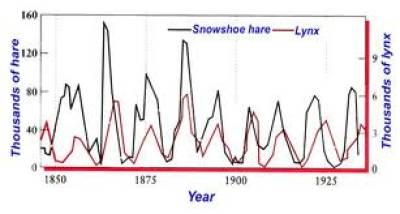 Nesse caso ambas as populações são controladas pela interação com a outra e não apenas pela relação com sua própria densidade.
Vamos primeiro analisar o modelo clássico de predador-presa desenvolvido independentemente por dois matemáticos na década de 1920, o americano Alfred Lotka e o italiano Vito Volterra.
Essas equações são relativamente simples:
Nesse caso ambas as populações são controladas pela interação com a outra e não apenas pela relação com sua própria densidade.
Vamos primeiro analisar o modelo clássico de predador-presa desenvolvido independentemente por dois matemáticos na década de 1920, o americano Alfred Lotka e o italiano Vito Volterra.
Essas equações são relativamente simples:
<box 70% red | Exercício 1: Interpretando os parâmetros >
O que significam os parâmetros da equação?
Seguindo a lógica dessas equações, qual sua solução com uma única espécie que cresce exponencialmente mas eventualmente se canibaliza? Você já viu essa equação?
</box>
Porque PV?
Para começar, baixe e carregue as funções que utilizaremos nesse roteiro predadorpizza.r 1)
Uma breve inspeção de cada uma das duas equações nos revela que, ignorando o termo com PV, elas são independentes, e simplificam para modelos exponenciais: crescimento exponencial para a presa e decrescimento exponencial para o predador.
Toda a interação das espécies em questão (no caso a predação) está então representada nesse termo. Que tipo de pressuposto leva a essa forma de interação?
Simulemos um predador que anda ao acaso em busca de presas dispostas aleatoriamente no espaço, por 25 passos, num grid de tamanho 50×50 com 1000 presas.
source("predadorpizza.r")
randomwalk(25,1000,50)
É evidente que quanto maior for a densidade de presas, menor será o intervalo entre os encontros e portanto entre os ataques (teste!), mas como será que se dá essa variação? A função a seguir (que pode demorar um pouco para rodar) retorna o tempo médio (calculado a partir de 100 repetições) para que o predador encontre uma presa (no grid 50×50), para quantidades de presas entre 400 e 1000.
tentreataques<-rdwsweep(ni=400,nf=1000,x=50,repe=100)
plotemos os dados obtidos a partir dessas simulações!
compr<-length(tentreataques)
plot(401:(400+compr),tentreataques, ylab="tempo médio entre ataques", xlab="número de presas")
Uhm… Parece familiar… A taxa de encontro é proporcional ao inverso do tempo de encontro! Plotemos isso então!
invtempo<-1/tentreataques
plot(401:(400+compr),invtempo,ylab="taxa de ataque média", xlab="número de presas")
npresas<-401:(400+compr)
modelo<-lm(invtempo~npresas)
abline(modelo, col=2, lwd=2)
De fato, supor movimento aleatório de um predador em meio a presas distribuídas ao acaso parece resultar em uma taxa de ataque que cresce linearmente com a densidade de presas, justificando o termo PV! É interessante notar que, embora não seja espacialmente explícito, a lógica por trás de Lotka-Volterra invoca um argumento de natureza espacial: a disposição e movimentação das presas e dos predadores.
Mas porque na hora de simular essa situação mantivemos as presas estáticas? Em primeiro lugar, porque para esse caso não haveria diferença no resultado, mas mais importantemente, por que isso permite uma flexibilização do modelo e a investigação de outras possibilidades.
As presas foram dispostas ao acaso, mas poderia haver algum comportamento que levasse a outras distribuições, mais agregadas, por exemplo. A imobilidade das presas nessa simulação permite que testemos o efeito dessas distribuições sem termos que nos preocupar com regras de movimento que mantivessem o padrão. Por hoje ficaremos apenas no padrão de distribuição aleatório.
/* A função rdwsweep tem um argumento inicializar, que recebe uma outra função, a qual posiciona as presas.
A função inicializa2 gera uma disposição agregada de presas. Ela pode ser dada como argumento para a rdwsweep chamando
rdwsweep(inicializar=inicializa2)
<box 70% red | Exercício 2: Distribuição das presas e a eficiência dos predadores>
Qual o efeito da distribuição gerada por inicializa2 na taxa de predação?
Plote ambas as taxas obtidas e seus respectivos modelos lineares.
Nessa perspectiva, a eficiência de ataque é uma propriedade apenas dos predadores?
Sinta-se livre, leve e solto para projetar suas próprias funções de distribuições e investigar suas consequências!
</box>
*/
Implementando o modelo
Vamos gerar a função básica para esse modelo no R:
ppLV <- function(times,y, parms)
{
V<-y[1]
P<-y[2]
with(as.list(parms),{
dH.dt <- b* V -a * P * V
dP.dt <- e * a* P*V -s *P
return(list(c(dH.dt,dP.dt)))
})
}
Dinâmica Lotka-Volterra
Vamos dar uma olhada como nesse sistema predador presa. Antes de tudo, vamos fazer o que é mais intuitivo para interpretar: um gráfico!
Primeiro vamos estabelecer os parâmetros da função e a situação inicial. Além disso precisamos dar o intervalos de iteração (parametro times):
parametros=c(a=0.01, b=0.5, e=0.1, s=0.2)
inic=c(V0=25,P0=5)
tempo=seq(0,100,by=0.1)
Agora só precisamos integrar numericamente a função, definindo os parâmetros o times e o estado incial com a função ode. Não esqueça, antes de tudo, de carregar o pacote deSolve. Além disso, vamos fazer um gráfico mostrando as trajetórias das populações.
require(deSolve)
vp.res1=ode(y=inic, times=tempo, func=ppLV, parms=parametros)
matplot(tempo,(vp.res1[,2:3]), type="l", main= "Dinâmica Predador-Presa", ylab="Tamanho da População")
Muito bem! Vamos em frente, fazer um gráfico com mais informações. Vamos criar outras duas trajetórias, com estados iniciais diferentes, e fazer um gráfico BONITO.
vp.res2=ode(y=c(V0=500,P0=15), times=tempo, func=ppLV, parms=parametros)
vp.res3=ode(y=c(V0=300,P0=50), times=tempo, func=ppLV, parms=parametros)
plot(vp.res1[,2], vp.res1[,3], type="l",main="Dinâmica Predador-Presa", ylab="Predador", xlab="Presa")
points(25,5 , cex=1.5, pch=19) # definindo no gráfico o estado incial das populações
arrows(x0=c(1300,-20,500), y0=c(125, 175, 0), x1=c(650,-20,950), y1=c(200,100,2), length=0.1)
lines(vp.res2[,2],vp.res2[,3] )
points(500,15,cex=1.5)
lines(vp.res3[,2],vp.res3[,3] )
points(300,50,cex=1.5, pch=2)
abline(h=parametros["b"]/parametros["a"],lty=2)
abline(v=parametros["s"]/(parametros["a"]*parametros["e"]),lty=2)
<box 70% red | Exercício 2: Interpretando o gráfico>
O que representa cada ponto nesse plano?
O que representam as curvas sólidas?
O que são as linhas pontilhadas?
Qual a importância do ponto de encontro delas?
Cada uma delas divide o plano em duas partes. Que comportamento caracteriza cada uma dessas partes?
</box>
Variações do Modelo: tempo discreto
No roteiro sobre competição vocês entraram em contato com o conceito de campo de direções de uma equação diferencial. Esse campo consiste de vetores que indicam a “direção” na qual a população está “caminhando” (se a quantidade de presas e predadores está aumentando ou diminuindo), e portanto é sempre tangente às trajetórias. A função orbitang permite que você plote uma órbita de um sistema Lotka-Volterra em pontos temporalmente equidistantes. Nesse caso, se os pontos estão próximos é porque a transição nessa parte da órbita é mais lenta. Testemos!
orbitang(nsetas=50,inic=c(V0=300,P0=100),parametros=c(a=0.01, b=0.5, e=0.1, s=0.2), fun=ppLV)
Você pode mudar os valores iniciais da órbita, os parâmetros da equação, o número de vetores do campo plotados e até a função em si (desde que as soluções ainda sejam periódicas, senão a função retorna erro…)
Brinque um pouco com os valores iniciais, parâmetros e o número de vetores plotados.
Note como eles sempre apontam para fora da órbita, não importa qual seja ela. Num modelo contínuo, como o que estamos integrando, os passos que a população dá (aumentos e decrescimentos populacionais) são infinitesimais, mas se fossemos resolver a equação discreta correspondente (nascimentos e mortes ocorrendo sincronicamente, e não continuamente), cada passada que a população desse na direção do campo da equação a levaria para uma outra órbita.
Que efeito você acha que isso teria sobre a população? Felizmente temos uma função no R para simular isso também!
LVdiscreto(parametros=c(a=0.01, b=0.5, e=0.1, s=0.2), inic=c(V0=200,P0=60), curvas=40, fun=ppLV)
A idéia de variação contínua e de variação discreta são extremos de um contínuo, algumas populações sendo bem representados por um tipo de modelo, outras pelo outro. Estamos assumindo um pressuposto razoavelmente irreal, no entanto: a passada do predador e da presa ocorrem ao mesmo tempo nesse modelo! É como se a estação reprodutiva do predador estivesse perfeitamente superimposta à da presa! Isso faz sentido? Mas podemos contemplar a possibilidade de as estações reprodutivas serem disjuntas adicionando o argumento assincrono=TRUE à função!
LVdiscreto(parametros=c(a=0.01, b=0.5, e=0.1, s=0.2), inic=c(V0=200,P0=80), curvas=60, fun=ppLV, assincrono=TRUE)
<box 70% red | Exercício 3: Problemática porque?>
Utilizando as funções dadas, simule sistemas predador-presa com mesmas características e compare ambos com o modelo contínuo.
Quais problemas podem ser apontados em relação a interpretação biológica desses modelos?
</box>
Modificações do Modelo: flutuações estocásticas
Seria ingênuo supor que populações vivas sigam modelos determinísticos de comportamento. Muitas variáveis ambientais afetam a performance dos seres em questão. Quando se deseja incorporar os efeitos de uma variável ambiental distintamente cíclica, como a temperatura, muitas vezes se lança mão de alguma função periódica como um seno ou cosseno.
Essa solução, no entanto negligencia a estocasticidade estrita. O modelo ainda é determinístico. Para incorporá-la a modelos de crescimento discreto podemos a cada iteração somar um pequeno ruído randômico. Para conseguir introduzir a estocasticidade a um modelo contínuo, podemos usar um caminho intermediário entre esses dois: criaremos uma função quasi-periódica, que se extende até o tempo máximo para o qual queiramos calcular a solução da equação, e cujos picos sejam randômicos.
Criemos um vetor de parâmetros com as constantes do modelo anterior (que não serão utilizadas na construção da função de ruído, mas devem ser passadas para o integrador), o tempo máximo para o qual definiremos o ruído, o número de “picos” que a função terá, e uma sequência de valores normalmente distribuídos com a média e variância escolhidos.
tmax=100
media=0
variancia=0.1
npicos=200
tmax=1000
parametrosruido=c(a=0.01, b=0.5, e=0.1, s=0.2,npicos,tmax,rnorm(npicos,media,variancia))
Podemos plotar a função curvabarulho que interpola esses valores de ruído
plot(1:tmax,curvabarulho(1:tmax,parametrosruido),type="l")
Note que toda vez em que rodamos a linha
parametrosruido=c(a=0.01, b=0.5, e=0.1, s=0.2,npicos,tmax,rnorm(npicos,media,variancia))
geramos uma nova trajetória do ruído, basta plotar de novo e verificar! Esse ruído foi incorporado à equação de predação através da função LVruido. Rodemos!
LVruido(inic=c(V0=300,P0=100), parametros=parametrosruido)
Veja que se rodarmos de novo a linha que gera os parâmetros, e depois a LVruido, sua trajetória será outra. Pela primeira vez as trajetórias contínuas se cruzam no espaço de fase! Porque?
Com a trajetória toda embolada é difícil saber o que ela faz no tempo… adicionemos mais um argumento: fabulous=TRUE
LVruido(inic=c(V0=300,P0=100), parametros=parametrosruido, fabulous=TRUE)
Agora podemos apreciar o vaivém da trajetória! O gradiente de cores representa a passagem do tempo, de modo que alças de cores distintas se cruzando refletem a natureza caótica (aqui pode chamar de caótica, Kraenkel?) do sistema!
Essa seção levanta uma problemática semelhante à da anterior.
<box 70% red | Exercício 4: Sobre Quasi-períodos >
</box>
Rosenzweig-MacArthur Model
O modelo de R&M inserem dois novos componentes na equação de Lotka-Volterra. Primeiro eles modelam que a presa, sem a presença do predador, seria autolimitada por um componente densidade dependente (p.ex:recurso limitante). Adicionalmente, nesse modelo, o predador apresenta uma saturação no consumo per capito com o aumento da densidade da presa. Neste caso, a resposta funcional é incluída de acordo com a função de Michaelis-Menten. Ou seja, com o aumento da quantidade de presa o predador aumenta o seu consumo por presa até um certo limite onde o aumento de presa não causa mais aumento de consumo per capitamente (p.ex. saciar apetite).
Vamos primeiro escrever a função para o Modelo R&M onde:
ppRM=function(t,y,parms)
{
V<-y[1]
P<-y[2]
with(as.list(parms),{
dV.dt <- b* V * (1-alfa * V) - w * P * V/(D+V)
dP.dt <- e * w* P*V/(D+V) -s *P
return(list(c(dV.dt,dP.dt)))
})
}
Agora vamos fazer um gráfico com o modelo e suas isolinhas. Primeiro vamos criar alguns parâmetros para o modelo.
b<-0.8
e<-0.07
s<-0.2
w<-5
D=400
alfa<-0.001
K=1/alfa
V<-0:K
Viso<-expression(b/w*(D+(1-alfa *D)*V-alfa*V^2))
VisoEv<-eval(Viso)
Vamos também criar uma trajetória dado um estado inicial. Para tanto precisamo integrar numericamente nosso modelo
param<-c(b=b,alfa=alfa, e=e,s=s,w=w,D=D)
tfinal=150
resPPRM<-ode(y=c(900,120),times=1:tfinal,func=ppRM, parms=param )
Finalmente vamos fazer o nosso gráfico:
plot(V,VisoEv,type="l", ylab="Predador", xlab="Vítima", ylim=c(0,150), col="red", lty=2, main="Modelo Rosenzweing-MacArthur")
abline(v=s*D/(e*w-s), lty=2, col="blue")
arrows(resPPRM[-tfinal,2], resPPRM[-tfinal,3], resPPRM[-1,2], resPPRM[-1,3], length=0.1)
<box 70% red | Exercício 5: Interpretando o gráfico, o retorno >
Interprete o gráfico que acabou de fazer
Aumente a capacidade suporte da presa para diferentes valores e veja como o sistema se comporta.
Para diferentes combinações de parâmetros (e.g. variando capacidade de suporte da presa) teste a função LVdiscreto. Os problemas foram resolvidos ou pelo menos mitigados?
</box>


