<html> <p style=“font: 14pt/20pt Garamond, Georgia, serif ;color:#ff9900; font-style:italic”>
Differential calculus is more interesting because it describes how things change.</p> </html>G. Evelyn Hutchinson citado por T.E. Lovejoy
Trataremos da revisão de três temas de Cálculo importantes para entendermos os modelos de dinâmica populacional apresentados durante a disciplina.
A idéia básica que queremos resgatar aqui é que ao estudarmos populações queremos entender e descrever como as populações variam no tempo. Não queremos apenas saber o tamanho da população em um dado tempo, mas como essa população muda ao longo do tempo. Essa é a idéia básica de taxas de variação que na matemática é traduzida como cálculo diferencial.
Assista o video de crescimento de bactérias abaixo: gEwzDydciWc?version=3?.swf
Agora, vamos descrever o processo de crescimento pelo número de bactérias observadas em tempos distintos:
| Tempo | No. de Bactérias |
|---|---|
| 0 | 2 |
| 1 | 4 |
| 2 | 8 |
| 3 | 16 |
| 4 | 32 |
| 5 | 64 |
| … | … |
| 14 | 16384 |
| … | … |
| 30 | 1073741824 |
| … | … |
| 60 | 1152921504606846976 |
É difícil entender o que está acontecendo, apenas olhando essa tabela. Uma forma mais sintética e compreensível de representar o crescimento das bactérias é através de um gráfico. Vamos fazer isso. Abra o R e siga o código abaixo:
tempo=1:10 nbact= c(2,4,8,16,32,64,128,256, 512,1024) plot(tempo, nbact) ## ficou feinho! Vamos fazer um mais bacana! plot(tempo, nbact, main="Crescimento de Bactérias", ylab= "número de bactérias", pch=16, col="red",cex.main=1.5, cex=1.5,cex.lab=1.5, cex.axis=1.5,bty="l")
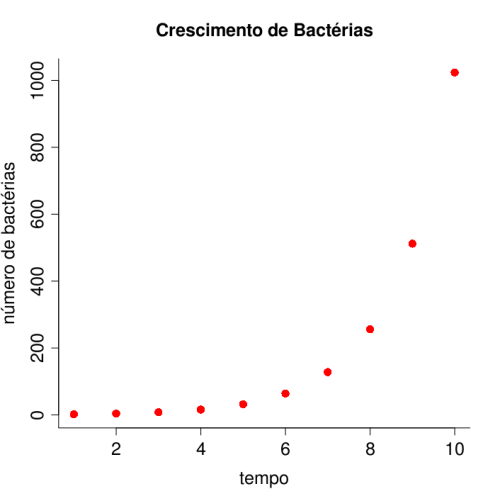
Note que o que temos são registros do tamanho da população em tempos discretos. Uma outra forma de descrever esse processo é saber:
Vamos então ver o quanto a população variou em um dado período de tempo, para isso vamos calcular uma taxa de variação:
$$ Taxa de Variação = \frac{N(t + \Delta t) - N(t)} {\Delta t} $$
Ou seja: pegue os valores do número de bactérias em dois tempos próximos e divida pelo tempo decorrido entre uma observação e outra!
Entretanto, o $ \Delta t $ é arbitrário. O que queremos é um valor instantâneo dessa taxa, o que independe do $ \Delta t $. Podemos portanto reduzir o $ \Delta t $ a valores muito pequenos de tempo,de forma que o $\Delta t$ tende a zero. Nessa situação, a diferença ${N_(t + \Delta t) - N_(t)}$ também tenderia a zero. Portanto, o resultado dessa taxa deve ser $ \frac{0}{0} $. É isso?
Vamos verificar se essa lógica está correta. Vamos definir a função que descreve nossos valores como $N(t)= t^2 $. Agora vamos reduzir o valor do $\Delta t$ para ver o que acontece com a taxa de variação quando $t=1$.
Antes porém vamos fazer o gráfico da função $N(t)= t^2 $, tendemos a entender melhor as fórmulas quando representadas graficamente.
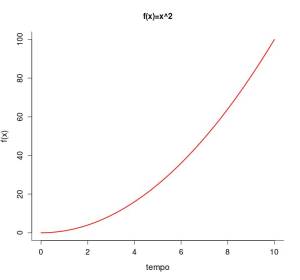
fn=function(x){x^2}
curve(fn, from=0,to= 10)
## para t=1 tempo=1 ##vamos criar um vetor com valores de delta t diminuindo dt=c(0.5,0.1,0.01,0.001,0.0001,0.00001,0.000001) tdt=tempo+dt Nt=tempo^2 Ntdt=tdt^2 (Ntdt-Nt)/dt
Estranhamente esse valor está convergindo para 2 e não para 0! Vamos fazer isso para outros tempos:
tempo=1:10 Nt=tempo^2 tdt=outer(tempo, dt, "+") Ntdt=tdt^2 Ntdt t(t(Ntdt-Nt)/dt)
Note que os valores de todos os tempos convergem da seguinte maneira quanto o $\Delta t \to 0 $:
| t | $\frac{N(t + \Delta t) - N(t)} {\Delta t} $ |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
| 5 | 10 |
Ou seja a taxa instantânea de crescimento da função $f(x) = x^2$ é igual a $2t$. Acabamos de calcular a primeira derivada. Vamos agora por convenção escrever a taxa de variação:
na forma de derivada:
Como a derivada se aplica a qualquer função vamos, a partir de agora usar uma notação mais geral:
Derivada da função $ f(x)$:
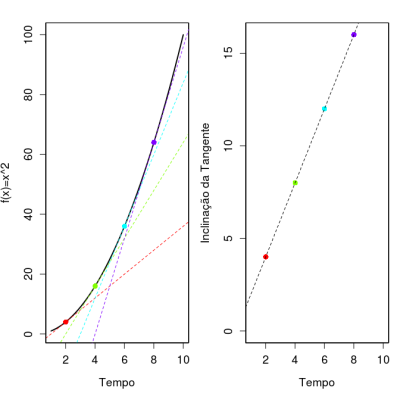Vamos agora fazer uma representação gráfica das taxas de variação instantâneas. Elas podem ser definidas como a inclinação da tangente da curva da função. Portanto, podemos desenhar as tangentes em alguns valores de tempo e depois representar graficamente os valores das inclinações em função do tempo.
fx=function(x){x^2}
par(mfrow=c(1,2))
curve(fx, from=1, to=10)
points(2,2^2, col="red", pch=16)
##############################
### calculando as inclinações
##############################
tx=seq(2, 8, by=2)
tmat=matrix(tx, ncol=7, nrow=4) ## quatro tempos, repetidos para fazer a soma
dt=c(0.5,0.1,0.01,0.001,0.0001,0.00001,0.000001)
dtmat=matrix(dt, ncol=7, nrow=4, byrow=TRUE)
Nt=tx^2
Ntmat=matrix(Nt, ncol=7, nrow=4)
tdt=tmat+dtmat
Ntdt=tdt^2
Ntdt
taxa = (Ntdt - Nt)/dtmat
taxa.diff=round(taxa[,7])
taxa.diff
a=Nt-taxa.diff*tx
#######################
## O Gráfico
#######################
cores=rainbow(length(tx))
par(mfrow=c(1,2))
curve(fx, from=1, to=10, ylab="f(x)=x^2", xlab="Tempo")
points(tx[1],fx(tx[1]), col=cores[1], pch=16)
abline(a[1], taxa.diff[1], col=cores[1], lty=2)
plot(tx, 2*tx , xlim=c(1,10),ylim=c(0,16), type="n", ylab="Inclinação da Tangente", xlab="Tempo")
points(tx[1], taxa.diff[1], pch=16, col=cores[1])
################################
### voltando ao primeiro gráfico
################################
par(mfg=c(1,1))
curve(fx, from=1, to=10, type="n", xaxt="n", yaxt="n",ylab="", xlab="")
points(tx[2],fx(tx[2]), col=cores[2], pch=16)
abline(a[2], taxa.diff[2], col=cores[2], lty=2)
par(mfg=c(1,2))
plot(tx, 2*tx , xlim=c(1,10),ylim=c(0,16), type="n", xaxt="n", yaxt="n",ylab="", xlab="")
points(tx[2], taxa.diff[2], pch=16, col=cores[2])
#######################
### Criando ciclos
#######################
for(i in 3:length(tx))
{
par(mfg=c(1,1))
curve(fx, from=1, to=10, type="n", xaxt="n", yaxt="n",ylab="", xlab="")
points(tx[i],fx(tx[i]), col=cores[i], pch=16)
abline(a[i], taxa.diff[i], col=cores[i], lty=2)
par(mfg=c(1,2))
plot(tx, 2*tx , xlim=c(1,10),ylim=c(0,16), type="n", xaxt="n", yaxt="n",ylab="", xlab="")
points(tx[i], taxa.diff[i], pch=16, col=cores[i])
}
abline(0,2, lty=2)
A partir do código acima, produzimos uma função no R para gerar as representações gráficas da função, suas tangentes e a derivada.
Essa função chamada deriva_tang1) tem três argumentos:
Vamos agora testá-la com algumas funções:
source("tang_function.r")
deriva_tang(expression(x^2))
deriva_tang(expression(x^3+ 3*x^2 -8), nder=20)
deriva_tang(expression(sin(x)*cos(x)), x.lim=c(-2,2), nder=100)
Apesar da cara do Chaves, parece que a função TANG não é tão azeda assim! Faça a figura de mais algumas funções e suas derivadas e interprete as inclinações, taxas e as distâncias entre os pontos do gráfico da esquerda.
A reta do gráfico acima tem a seguinte função (2) $ y = 2x $. Essa é a derivada da função (1) $f(x)=x^2$. Ou seja, a derivada de uma função (quadrática) é uma outra função (linear) que descreve a variação da taxa instantânea da primeira. Entre outras coisas, a disciplina de cálculo lida com a derivação de funções, ou o cálculo diferencial. Não necessitamos fazer todos os procedimento de iteração anteriores para chegar a uma aproximação da derivada de uma função. Algumas regras nos ajudam a calcular a derivada rapidamente,são regras que devemos decoradas para que depois possamos operar e calcular a derivada.
Abaixo listamos as principais regras do cálculo de derivadas. A primeira é bem simples e intuitiva, uma função constante não tem variação e sua inclinação é zero!
A derivada de uma constante é zero
A derivada de uma função linear é uma constante definida pela inclinação da reta
Essa regra foi o nosso exemplo acima. A derivada de uma função quadrática é uma função linear:
É a generalização da função quadrática, ou mesmo da função linear:
* onde: $ a, b, c,… z $ são constantes
Como pode ser deduzido da regra acima, a derivada de um polinômio de grau $n$ é uma função polinômial de grau $n-1$.
A derivada da soma de duas funções e a soma de suas derivadas:
Use as regras acima e encontre as derivadas das seguintes funções:
| Exercícios na Mão |
|---|
Em nossas aulas de revisão de cálculo vamos usar uma ferramenta muito útil, o programa Maxima. O Maxima é CAS (Computer Algebra System) semelhante a sistemas como o Mathematica, Maple e outros que trabalham com expressões simbólicas, com a vantagem de ser um programa de código aberto. Ele opera, não apenas números, mas as próprias expressões matemáticas, o que é uma mão na roda. No final, não precisamos decorar todas as regras de cálculo. Tenha em mente que, quando tiver um problema de cálculo, pode utilizar esse tipo de programa para obter soluções de expressões complicadas. Entretanto, para utilizar as ferramentas deve entender o quê está fazendo, porquê está fazendo e para quê!
Abaixo o linque do site para baixar o Maxima:
O Máxima já vem com uma interface gráfica para usuário chamada wxMaxima. Para usuários de sistemas Linux (Ubuntu e outros) o wxMaxima está disponível diretamente nos repositórios Debian.
Neste tutorial introdutório 3), você vai aprender o básico do wxMaxima e Maxima. Vamos fazer um tutorial básico seguido da conferência dos resultados dos exercícios acima!
Abra o arquivo abaixo no Maxima e tente acompanhar os passos, lembrando o que foi apresentado em aula. Qualquer dúvida, lembre-se de usar o F1 (help) do wxMaxima.
