Neste exercício testaremos vários modelos que tentam explicar a relação espécies-área.

“A relação espécies-área é uma das poucas leis genuínas em ecologia” (Gotelli, 2007). O que você acha desta afirmação? Será que podem existir leis em ecologia? Vamos conferir!

Que tal agora darmos um passeio pelo mundo “real”? Vamos ver alguns dados reais, coletados por pessoas reais em lugares reais. Então é tudo verdade, ok? Rode os comandos no R para ver os tais dados.

# Número de espécies endêmicas de plantas vasculares em nove localidades da Califórnia.

# Dados
calif=data.frame(
  local=c("Tiburon","SanFran","StaBarbara","StaMonica","Marin",
    "StaCruz","Monterey","SanDiego","California"),
  area=c(5.9,45,110,320,529,1386,3324,4260,24520),
  riqueza=c(370,640,680,640,1060,1200,1400,1450,2525)
  )
calif

# Gráfico
plot(riqueza~area,data=calif,xlab="Área",ylab="Número de espécies",main="Menina eu vou pra Califórnia...",
 bty="l",font.lab=2)

A lei da relação espécies-área é empírica, ou seja, foi descrita a partir de dados como os acima. A relação acima pode ser descrita por uma função de potência: <m>S=c A^z</m> , onde S é o número de espécies, A é a área e c e z são constantes. Veja o gráfico dessa função:

x11()
curve(expr = 2.39*x^.22 , from=0, to=25000, xlab="Área",
	 ylab="Número de espécies", font.lab=2, lwd=2, col=2)

Agora observe o que acontece quando transformamos as escalas do gráfico em logaritmos:

# Gráfico
plot(riqueza~area,data=calif,log="xy",xlab="Área",ylab="Número de espécies",main=c("Menina eu vou pra Califórnia...",
 paste("c = ",round(mod[[1]][1],2),"; z = ",round(mod[[1]][2],2))),bty="l",font.lab=2)


# Ajuste da reta
mod=lm(log10(riqueza)~log10(area),data=calif)
mod
abline(mod,col=2)

Note que o que era uma função de potência, na escala logaritmica vira uma equação de reta: <m |>log(S)=log©+z log(A)</m> .

Esses dados, de espécies de plantas vasculares endêmicas em regiões da California foram coletados por Johnson e colaboradores e publicados em um trabalho em 1968 (ver referências no fim da página). Estão disponíveis neste site .

Agora vamos brincar um pouco com a relação espécies-área variando os parâmetros c e z. Rode os comandos abaixo:

spp.area=function(c , z){
	curve(expr = c*x^z , from=1, to=10^10, xlab="Área", ylim=c(1,500),
	 ylab="Número de espécies", font.lab=2, lwd=2, col=2, main=paste("c = ",c,"; z = ",z))
	curve(expr = c*x^z , from=1, to=10^10, xlab="Área", ylim=c(1,500),
	 ylab="Número de espécies", font.lab=2, lwd=2, col=2, main=paste("c = ",c,"; z = ",z), log="xy")
	}

par(mfrow=c(2,2))
spp.area(c = 1.5 , z = .25)
spp.area(c = 2.1 , z = .25)

Note que os dois eixos do gráfico da direita estão em escala logarítmica. Note também que a função lhe permite variar os dois parâmetros da equação: c e z. Altere os valores desses parâmetros e veja o que acontece. Você consegue pensar em um significado biológico para esses dois parâmetros?

Lembra da aula de metacomunidades? Lembra que a extinção e a imigração eram parte importante da dinâmica populacional de uma espécies que ocorria em manchas? Aqui faremos basicamente a mesma coisa, só que desta vez consideraremos várias espécies ao mesmo tempo e em vez do tamanho da população nosso interesse será o número de espécies em cada mancha, que no caso serão ilhas.

Neste exercício usaremos o sistema ilha-continente, que é equivalente à chuva de propágulos do exercício de metacomunidades. Nesse sistema, há uma ilha (mais para frente será um arquipélago!) que pode receber propágulos vindos do continente, que assumiremos como um reservatório de n espécies e como uma fonte infinita de propágulos.

Você gostaria de viver em uma ilha de fantasia? Eu também, mas primeiro você deve chegar lá: ou você tem que ser bom nadador ou ser muito rico e chegar de iate. Com as espécies de planta é a mesma coisa, mas vamos assumir por ora que todas as espécies tem a mesma probabilidade de chegar à ilha. (Será que isso acontece no mundo real? Você acha que as chances de uma espécie dispersa pelo vento de chegar a uma ilha são iguais às de uma espécie dispersa por macacos? Será que macacos são bons nadadores?)

Imagine que a cada momento chega um determinado número de propágulos vindos do continente à nossa ilha. Se é assim, é de se esperar que com o passar do tempo todas as espécies presentes no continente estejam também presentes na nossa ilha, certo? Quer ver se isso é verdade? A seguir vamos simular um sistema ilha-continente.

Neste primeiro exemplo, o continente possui duas espécies (A e B), cada espécie tem dez indivíduos e cada indivíduo contribui com uma semente por vez. Assim, todos os propágulos disponíveis no continente a cada momento é:

cont=rep(c("A","B"),each=10)
cont

Digamos que só conseguem fazer a travessia 50% das sementes, ou seja, 50% das sementes se perdem no caminho. No nosso exemplo teremos, então, apenas 10 sementes chegando à ilha.

table(sample(cont,10,replace=T))

Repita o código acima e veja se a composição do conjunto de propágulos que chegam à ilha é sempre a mesma. (A partir de agora vamos chamar cada conjunto de propágulos que chegam de “chuva”.)

chuva=sample(cont,10,replace=T)
table(chuva)

Vamos imaginar agora que a espécie A é anemocórica (dispersa pelo vento) e tem muito mais chance de chegar à ilha do que a espécie B. (Você pode imaginar também que ambas são anemocóricas, porém há muito mais indivíduos da espécie A no continente do que da espécie B.)

chuva=sample(c("A","B"),10,replace=T,prob=c(.5,.1))
table(chuva)

# O argumento //prob// diz qual a chance de cada espécie chegar à ilha.

A composição da chuva mudou? Vamos agora aumentar o número de espécies no continente para dez e ver o que acontece (cada espécie terá a mesma chance de chegar à ilha neste exemplo).

cont=rep(LETTERS[1:10],each=10)
cont
chuva=sample(cont,10,replace=T)
table(chuva)

Você notou que praticamente nunca todas as espécies estão presentes na chuva? Isso era esperado, afinal a probabilidade de termos uma chuva de 10 sementes com 1 semente de cada espécie é:

(1/10)^10

Ou seja, muitissíssimo baixa!

Antes de continuarmos, vamos fazer um exercício de imaginação. Pense nas espécies como figurinhas (tá, as figurinhas não precisam ser de jogadores do Vasco da década de 80), pense nas ilhas desertas como álbuns vazios e pense na chuva de propágulos como pacotinhos de figurinhas vindos da fábrica de figurinhas (a nossa fonte de propágulos). Se em cada pacote vêm 5 figurinhas, quanto tempo leva para completar um álbum com 100 figurinhas? Vamos assumir que que o dono da empresa de figurinhas não é sacana e produz a mesma quantidade de cada uma dos 100 tipos diferentes de figurinha e também que você é meio mão-de-vaca e compra no máximo um pacote por vez.

# Primeiro criamos todas as figurinhas possíveis

figu=paste("fig.",1:100,sep="")
figu

# Agora simulamos uma ida à banca

# Um pacote
sample(figu,5,replace=T)
# Outro pacote
sample(figu,5,replace=T)
# E mais outro
sample(figu,5,replace=T)

Vamos simular uma viagem no tempo e ver o que aconteceu depois de 1000 idas à banca.

album=numeric()
cpl=numeric()
for(i in 1:1000){
	album=union(album,sample(figu,5,replace=T))
	cpl[i]=length(unique(album))
	}
plot(1:1000,cpl,xlim=c(0,500),ylim=c(0,100),type="l",bty="l",
 xlab="Número de pacotes",ylab="Número de figurinhas (excluindo as repetidas)",
 main="Álbum de figurinhas",lwd=2,col=2,font.lab=2)
abline(h=100,lty=3)

Através de uma simulação como essa podemos ter idéia de quantos pacotinhos teremos que comprar para completar o álbum. Mais um serviço de utilidade pública! Note que a velocidade com que o álbum vai sendo preenchido vai ficando cada vez menor. A gente já sabia disso: quanto mais figurinhas temos, mais repetidas saem.

Mas completar esse álbum foi muito fácil! Isso nunca ocorre na vida real! Mas e se fôssem mais figurinhas? E se eu comprasse mais pacotes por vez? E se houvesse algumas figurinhas mais raras? Para responder a estas e muitas outras perguntas criamos a função abaixo.

chove.chuva=function(Nspp , chuva , abund , tempo){
	spp=paste("sp.",1:Nspp)
	ilha=numeric()
	riq=numeric()
	for(i in 1:tempo){
		ilha=union(unique(sample(spp,chuva,replace=T,prob=abund/sum(abund))),ilha)
		riq[i]=length(ilha)
		}
	plot(0:tempo,c(0,riq),type="l",lwd=2,bty='n',xlab="tempo",ylab="número de espécies",
	 font.lab=2,col=2,ylim=c(0,Nspp),main=c("Riqueza da ilha",paste("(Nspp=",Nspp," ; chuva=",chuva,")")))
	abline(h=Nspp,lty=3)
	return(riq)
	}

# faça um teste:
chove.chuva(Nspp=10, chuva=10, abund=c(10,10,10,10,10,10,10,10,10,10), tempo=10)

Agora vamos simular alguns casos particulares:

# 100 espécies, chuva traz 5 propágulos por ano, no continente há 100 propágulos para cada espécie e irão se passar 100 anos.

chove.chuva( Nspp = 100 , chuva = 5 , abund = rep(100,100) , tempo = 100)

Agora, digamos que no continente há 100 indivíduos de uma única espécie e 99 espécies com apenas um indivíduo:

chove.chuva( Nspp = 100 , chuva = 5 , abund = c(100,rep(1,99)) , tempo = 100)

Voltando ao exemplo das figurinhas, imagine em quanto aumentaria o lucro do dono da fábrica de figurinhas se ele produzisse um número menor de certas figurinhas. (Maldito! Certeza que ele fazia isso! )

Para fechar esta seção de imigração, vamos calcular a taxa de imigração: o número de espécies novas que chegam à ilha por unidade de tempo (ou a quantidade de figurinhas novas que vêm em cada pacotinho):

# Comunidade igualitária - todas as espécies com o mesmo número de indivíduos no continente
riq1=chove.chuva( Nspp = 100 , chuva = 5 , abund = rep(100,100) , tempo = 100)
riq1
tx.imig=numeric()
for(i in 1:100){tx.imig[i]=(riq1[i]-riq1[i-1])}
tx.imig[1]=riq1[1]
tx.imig

# Gráfico
plot(1:100,tx.imig,type="l",font.lab=2,xlab="Tempo",
 ylab="Número de espécies novas",main=c("Taxa de imigração","Nspp = 100 ; chuva = 5"),
 bty="l",lwd=2,ylim=c(0,10))
tempo=1:100
abline(lm(tx.imig~tempo),col=2,lwd=2)

# Muitos têm pouco e poucos têm muito - uma espécie muito abundante e várias raras no continente
riq2=chove.chuva( Nspp = 100 , chuva = 5 , abund = c(100,rep(1,99)) , tempo = 100)
riq2
tx.imig2=numeric()
for(i in 1:100){tx.imig2[i]=(riq2[i]-riq2[i-1])}
tx.imig2[1]=riq2[1]
tx.imig2

# Gráfico
plot(1:100,tx.imig2,type="l",font.lab=2,xlab="Tempo",
 ylab="Número de espécies novas",main=c("Taxa de imigração","Nspp = 100 ; chuva = 5"),
 bty="l",lwd=2,ylim=c(0,10))
abline(lm(tx.imig2~tempo),col=2,lwd=2)

Para comparar melhor refaça os gráficos, mas antes use par(mfrow=c(2,2)).

Foi muito fácil até agora? Que tal complicar um pouquinho então? Veremos agora o modelo mais simples capaz de explicar a relação espécies-área. A idéia é simples: o tamanho da ilha determina a quantidade de propágulos que ela é capaz de interceptar. Difícil de imaginar? Não é mais: pense que sua casa estava cheia de goteira, como a do lado, e que você colocou todos os recipientes disponíveis para captar a água que pingava. Qual destes objetos você acha que interceptava mais gotas: um copo, uma panela ou uma bacia? O princípio é o mesmo! Só que em vez de gotas temos propágulos e em vez de panelas, ilhas.

Então, se este modelo estiver correto, poderemos prever quantas espécies existem em cada uma das ilhas de um arquipélago. Vamos começar criando 10 ilhas de diferentes tamanhos:

areas=c(1,5,10,50,100,500,1000,2000,2500,5000)
names(areas)=LETTERS[1:10]
areas

Qual dessas ilhas você espera que tenha o maior número de espécies? Para tornar sua vida mais doce, pode usar a função abaixo. Fique atento porque esta função cria dois gráficos a cada vez que é rodada.

arquip=function(areas, Nspp, chuva.total, abund, tempo){
	n.ilhas=length(areas)
	spp=paste("sp.",1:Nspp)
	ilhas=paste("Ilha",1:n.ilhas)
	chuva=round(chuva.total*areas/sum(areas))
	riq=numeric()
	
	par(mfrow=c(ceiling(sqrt(n.ilhas)),ceiling(sqrt(n.ilhas))))
	for(i in 1:n.ilhas){
		riq[i]=chove.chuva(Nspp,chuva[i],abund,tempo)[tempo]
		}
	names(riq)=ilhas
	mod=lm(log10(riq)~log10(areas))
	x11()
	plot(areas,riq,log="xy",font.lab=2,pch=16,col=2,bty="l",
		main=paste("Nº ilhas=",n.ilhas,"; Nº spp=",Nspp,"; tempo=",tempo),
		xlab="Área da ilha",ylab="Número de espécies",ylim=c(1,Nspp))
	abline(mod,lty=2)

	cat("c=",mod[[1]][1],"z=",mod[[1]][2],"\n")
	return(riq)
	}

arquip(areas=c(10,20,40,80),Nspp=1000,chuva.total=100,abund=rep(10,1000),tempo=10)

Note que a função retorna o número de espécies de cada ilha e os parâmetros c e z da relação espécies-área (lembra?).

E aí? O modelo é capaz de explicar a relação espécies-área?

No meu tempo, tínhamos que colar as figurinhas no álbum com cola. Sempre usávamos cola branca (yami!), porque usar cola de bastão era garantir que perderíamos algumas figurinhas pelo caminho. Vamos imaginar que nossas figurinhas, depois de coladas, têm uma certa chance de descolarem e se perderem. Como fica nosso modelo?

No nosso modelo antigo, que não considerava a possibilidade de extinção, a ilha ficava sempre com o mesmo número de espécies do continente. Mas será que isso faz sentido? As espécies não podem se extinguir? O dodô, uma ave não voadora que habitava as ilhas Maurícias, é uma prova disto. Então vamos adaptar a função preexistente chove.chuva para que ela passe a exterminar algumas espécies ao acaso.

dançando.na.chuva=function(Nspp, chuva, abund, tempo, tx.ext){
	spp=paste("sp.",1:Nspp,sep="")
	ilha=numeric()
	riq=numeric()

	ilha=unique(sample(spp,chuva,replace=T,prob=abund/sum(abund)))
	riq[1]=length(ilha)

	for(i in 2:tempo){
		rr=sample(c("V","M"),length(ilha),replace=T,prob=c((1-tx.ext),tx.ext))
		roleta=data.frame(ilha,rr)
		vivos=roleta[roleta$rr=="V",1]
		ilha=union(sample(spp,chuva,replace=T,prob=abund/sum(abund)),vivos)
		riq[i]=length(unique(ilha))
		}

	
	plot(0:tempo,c(0,riq),type="l",lwd=2,bty='n',xlab="tempo",ylab="número de espécies",
	 font.lab=2,col=2,ylim=c(0,Nspp),
	 main=c("Riqueza da ilha",paste("Nspp =",Nspp," ; chuva =",chuva,"; tx.ext = ",tx.ext)))
	abline(h=Nspp,lty=3)
	
	return(riq)
	}

Vamos ver se deu tudo certo? Primeiro vamos testar com alguns parâmetros pré-definidos, mas depois você, ao contrário do dodô, estará livre para voar e fazer a combinação que você quiser!

dançando.na.chuva(Nspp=100, chuva=5, abund=rep(100,100), tempo=100, tx.ext=.1)

Ahã! Agora parece que ficou beeeem mais difícil completar o álbum, não é mesmo?! Será que é possível completá-lo? Note que a taxa de extinção é de apenas 10%!!! Vamos dar um pouco mais de tempo:

dançando.na.chuva(Nspp=100, chuva=5, abund=rep(100,100), tempo=1000, tx.ext=.1)

O que está acontecendo aqui??? O que acontece quando aumentamos a taxa de extinção? E se aumentamos a chuva? E se a disponibilidade de propágulos não fôr a mesma para todas as espécies? Será que o dono da fábrica de figurinhas é macomunado com o dono da fábrica de cola? Estas e muitas outras perguntas surgirão, mas não as guarde para si. Exponha suas dúvidas aos colegas e explore as funções criadas.

A idéia básica deste modelo é que o número de espécies de uma ilha é um balanço entre a imigração de novas espécies vindas do continente e a extinção das espécies presentes. Quando as taxas de imigração ($$ \lambda $$) e extinção ($$\mu$$) se igualam, o número de espécies (S) atinge um equilíbrio dinâmico:

$$\frac{dS}{dt} \ = \ \lambda-\mu$$

O modelo assume que quanto mais espécies presentes na ilha, menor é a chegada de novas espécies do continente. Lembra de como vai ficando cada vez mais difícil encontrar figurinhas que não sejam repetidas? Pois é, o princípio é o mesmo. Neste modelo a função que descreve a taxa de imigração é:

$$\lambda=I-(I/P)\ S$$ ; onde I é a taxa de imigração máxima (quando a ilha está deserta) e P é o número de espécies no continente. Faça o gráfico:

I = 0.5 ; P = 100
curve(I-I*x/P,0,P,bty="n",xaxt="n",yaxt="n",xlab="Número de espécies",
 ylab="Taxa de imigração",font.lab=2,lwd=2)
abline(v=0)
abline(h=0)
mtext("P",side=1,at=P,font=2)
mtext("I",side=2,at=I,font=2,las=1)

O modelo assume também uma taxa de extinção. Supondo que todas as espécies tenham uma mesma e constante taxa de extinção, esperamos que quanto maior o número de espécies presentes, maior o número de espécies que se extinguirá. É como na loteria: se cada bilhete tem uma certa probabilidade de estar premiado, quanto mais bilhetes você comprar, mais chances tem de ganhar. Vamos à equação da taxa de extinção:

$$\mu=(E/P)S$$ ; onde E é a taxa máxima de extinção, que ocorre quando o número de espécies da ilha é igual ao do continente. Veja o gráfico:

E = 0.8 
curve((E/P)*x,0,P,bty="n",xaxt="n",yaxt="n",xlab="Número de espécies",
 ylab="Taxa de extinção",font.lab=2,lwd=2)
abline(v=0)
abline(v=P,lty=3)
abline(h=0)
abline(h=E,lty=3)
mtext("P",side=1,at=P,font=2)
mtext("E",side=2,at=E,font=2,las=1)

Juntando tudo…

$${dS}/{dt}\ = \ I-(I/P)\ S-(E/P)\ S$$

…e batendo no liquidificador, teremos:

$$S \ = \ \frac{ I P }{I+E}$$

$$T \ = \ \frac{ I E }{I+E}$$

que são, respectivamente, o número de espécies no equilíbrio (S) e a taxa de substituição de espécies no equilíbrio (T). Note que este não é um equilíbrio estático, isto é, apesar de o número de espécies permanecer constante, a composição de espécies está sempre se alterando, com novas espécies chegando e velhas espécies se extinguindo.

Utilize a função abaixo para criar um gráfico do modelo:

grafeq=function(E , I , P){
	S = I*P/(I+E) ; T = I*E/(I+E)
	curve(I-I*x/P,0,P,bty="n",xaxt="n",yaxt="n",xlab="Número de espécies",
	 ylab="Taxas",font.lab=2,lwd=2,ylim=c(0,1))
	curve((E/P)*x,0,P,lwd=2,add=T)
	abline(v=0)
	abline(h=0)
	mtext("P",side=1,at=P,font=2)
	mtext("I",side=2,at=I,font=2,las=1)
	mtext("E",side=4,at=E,font=2,las=1)
	mtext("S",side=1,at=S,font=2,col=2)
	mtext("T",side=2,at=T,font=2,las=1,col=2)
	points(S,T,col=2,pch=16,cex=1.3)
	segments(S,T,S,0,lty=3,col=2)
	segments(S,T,0,T,lty=3,col=2)
	}

# testando...
grafeq(E = .5 , I = .5 , P = 100)

Agora experimente mudar os valores de E, I e P. O que acontece com o ponto de equilíbrio? Para dar uma mãozinha, desenvolvemos estas (des)animações:

# aumentando apenas E
a=seq(from=.01,to=1,by=.01)
for(i in 1:100){
	grafeq(E=a[i],I=.5,P=100)
	Sys.sleep(.04)
	}

# aumentando apenas I
for(i in 1:100){
	grafeq(E=.5,I=a[i],P=100)
	Sys.sleep(.04)
	}

# aumentando I e E
for(i in 1:100){
	grafeq(E=a[i],I=a[i],P=100)
	Sys.sleep(.04)
	}

# aumentando I e diminuindo E
b=seq(from=1,to=.01,by=-.01)
for(i in 1:100){
	grafeq(E=b[i],I=a[i],P=100)
	Sys.sleep(.04)
	}

# aumentando E e diminuindo I
for(i in 1:100){
	grafeq(E=a[i],I=b[i],P=100)
	Sys.sleep(.04)
	}

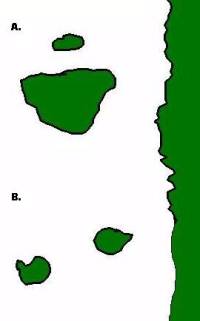Até aqui tudo correu bem? Pois então vamos brincar um pouco mais com nosso modelo, desta vez trabalhando com mais de uma ilha ao mesmo tempo. Nosso primeiro caso será o de duas ilhas igualmente distantes da costa, mas com diferentes tamanhos, como no topo da figura ao lado (A). Neste caso, vamos assumir que a probabilidade de imigração não difere entre as ilhas, afinal elas estão à mesma distância do continente. No entanto, assumiremos que a taxa de extinção será maior na ilha menor. Será que isso faz sentido? Imagine que quanto menor a ilha, menor o número de indivíduos que cabe nela e, assim, maior a chance de uma população se extinguir. Agora parece razoável?

Nosso segundo exemplo será o de duas ilhas de mesmo tamanho, mas que estão a distâncias diferentes da costa,como no fundo da figura ao lado (B). Agora o problema passa a ser a chegada de novos propágulos: é razoável supor que quanto mais distante uma ilha fôr do continente, menor a taxa de imigração? Neste caso como têm praticamente a mesma área, as duas ilhas tem taxas de extinção semelhantes.

Doeu muito? Se sim, valeu a pena porque agora você pode dizer que finalmente entendeu a teoria de biogeografia de ilhas de MacArthur e Wilson! É…, mas o quê? Isso não quer dizer nada para você? Pôxa, mas você podia ter disfarçado pelo menos! Bom, de qualquer forma criamos uma função bem bacana. Com ela você poderá fazer a combinação de ilhas que você quiser e ver se no final consegue encontrar uma relação espécies-área (lembra?). Afinal foi para explicar essa relação que esta teoria foi criada.

Antes de criar a função, vamos criar uma relação negativa entre área da ilha e taxa de extinção:

a = 1 ; b = -.01
curve(a+b*x,0,100,bty="l",xlab="Área da ilha",
	 ylab="Taxa de extinção",font.lab=2,lwd=2,ylim=c(0,1))

# E uma relação entre taxa de imigração e distância do continente:
c = 1 ; d = -.01
curve(c+d*x,0,100,bty="l",xlab="Distância da ilha ao continente",
	 ylab="Taxa de imigração",font.lab=2,lwd=2,ylim=c(0,1))

Finalmente a função:

MW=function(areas , dist , P , a=1, b=-.01, c=1, d=-.01){
  par(mfrow=c(1,2))
  E=a+b*areas
  I=c+d*dist
  S=numeric()
  for(i in 1:length(areas)){S[i]=I[i]*P/(I[i]+E[i])}
  T=numeric()
	for(i in 1:length(areas)){T[i]=I[i]*E[i]/(I[i]+E[i])}
  
  curve(I[1]-I[1]*x/P,0,P,bty="n",xaxt="n",yaxt="n",xlab="Número de espécies",
        ylab="Taxas",font.lab=2,lwd=2,ylim=c(0,1))
  curve((E[1]/P)*x,0,P,lwd=2,add=TRUE)
  abline(v=0)
  abline(h=0)
  mtext("P",side=1,at=P,font=2)
  mtext("I1",side=2,at=I[1],font=2,las=1)
  mtext("E1",side=4,at=E[1],font=2,las=1)
  mtext("S1",side=1,at=S[1],font=2,col=2)
  mtext("T1",side=2,at=T[1],font=2,las=1,col=2)
  points(S[1],T[1],col=2,pch=16,cex=1.3)
  segments(S[1],T[1],S[1],0,lty=3,col=2)
  segments(S[1],T[1],0,T[1],lty=3,col=2)
  
  for(i in 2:length(areas)){
    curve(I[i]-I[i]*x/P,0,P,lwd=2,ylim=c(0,1),add=TRUE,lty=i)
    curve((E[i]/P)*x,0,P,lwd=2,add=TRUE,lty=i)
    mtext(paste("I",i,sep=""),side=2,at=I[i],font=2,las=1)
    mtext(paste("E",i,sep=""),side=4,at=E[i],font=2,las=1)
    mtext(paste("S",i,sep=""),side=1,at=S[i],font=2,col=i+1)
    mtext(paste("T",i,sep=""),side=2,at=T[i],font=2,las=1,col=i+1)
    points(S[i],T[i],col=i+1,pch=16,cex=1.3)
    segments(S[i],T[i],S[i],0,lty=3,col=i+1)
    segments(S[i],T[i],0,T[i],lty=3,col=i+1)
  }
  
  ex=data.frame(areas=areas,spp=S,dist=dist)
  y=lm(S~areas)[[1]][1]
  z=lm(S~areas)[[1]][2]	
  plot(spp~areas,data=ex,log="xy",font.lab=2,pch=as.character(1:length(areas)),col=2,bty="l",
       main=c("Equilíbrio de M&W",paste("c = ",round(y,2),"; z = ",round(z,2))),
       xlab="Área da ilha",ylab="Número de espécies",ylim=c(1,P))
  abline(lm(log10(spp)~log10(areas),data=ex),lty=3)
  
  return(ex)
  par(mfrow=c(1,2))
}

Muito bem, agora você pode continuar se divertindo com o modelo fazendo as mais loucas combinações.

Que tal testar a teoria? Será que ela é capaz de explicar a relação espécies-área? Confira a seguir:

# Ilhas com diferentes áreas, mas com as mesmas distâncias
MW(areas=c(1,15,30,60,90) , dist=rep(50,5) , P=100)

# Ilhas com as mesmas áreas, mas com diferentes distâncias
MW(areas=rep(50,5) , dist=c(1,15,30,60,90) , P=100)

Percebeu que nem sempre as ilhas com mais espécies são as que possuem maior taxa de substituição de espécies?

Agora vamos variar área e distância ao mesmo tempo!

# Ilhas com diferentes áreas e distâncias
MW(areas=c(1,15,30,60,90) , dist=c(90,60,30,15,1) , P=100)
MW(areas=c(1,15,30,60,90) , dist=c(1,15,30,60,90) , P=100)
MW(areas=c(1,10,15,30,45) , dist=c(2,20,30,60,90) , P=100)

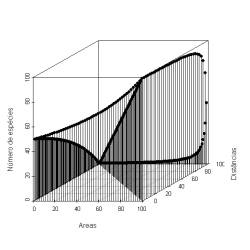Ops! O que aconteceu? Parecia estar indo tão bem… Calma, nada de pânico. Na verdade, neste segundo exemplo incorporamos um fator que não é considerado na relação espécies-área: as distâncias. Para tanto seria preciso um terceiro eixo contendo as distâncias entre as ilhas e os continentes e aí não teríamos mais uma reta descrevendo o padrão, mas sim uma superfície. Veja ao lado como fica um gráfico em três dimensões usando inúmeras ilhas imaginárias. Veja como é complexa a forma da superfície que descreve a relação espécies-área-distância!

<box 60% red|Atenção!> Só prossiga se você estiver com tempo. Se não fôr o caso vá primeiro para a seção “Teoria neutra da biodiversidade”. Não fique triste, você ainda pode fazer o resto em casa, tipo na sexta ou no sábado à noite… Lembrando que o autor deste roteiro não se responsabiliza por eventuais danos causados à nota do seu questionário. </box>

Como diria o ditado, para quê simplificar se podemos complicar! Até agora consideramos o efeito da distância e do tamanho da ilha, só que a distância só tinha efeito sobre a taxa de imigração e o tamanho só tinha efeito na taxa de extinção. Mas será que distância não pode afetar também a taxa de extinção? E o tamanho da ilha não pode alterar a taxa de imigração? Veja a seguir.

Este é um velho conhecido de vocês: lembra da aula prática de metapopulações? Lembra o que é o efeito resgate? Bem, como relembrar é viver aí vai: efeito resgate, como o nome diz, é o resgate de uma população à beira da extinção. No nosso caso, o resgate é feito por propágulos vindos do continente e que ao chegar à ilha impedem que a espécie se extingua. Se a ilha é muito distante do continente, a chegada desses novos propágulos é bem pouco provável. Neste caso praticamente não teríamos o efeito resgate, resultando em uma taxa de extinção basal (aquela que já tínhamos inserido no modelo antes). Por outro lado, se a ilha estiver bem perto do continente, será grande a quantidade de propágulos que chegará à ilha, fazendo com que a taxa de extinção real seja bem menor do que a taxa de extinção basal. Vamos deixar de conversa e pôr o efeito resgate em prática! Primeiro, vamos estabelecer uma relação entre taxa de imigração e distância da ilha ao continente:

g = 0 ; h = .01
curve(g+h*x,0,100,bty="l",xlab="Distância da ilha ao continente",
	 ylab="Taxa de extinção",font.lab=2,lwd=2,ylim=c(0,1))

Agora, vamos ao segundo efeito complicador do nosso modelo, o efeito de alvo.

Este efeito também já foi apresentado, porém mais recentemente. Consegue lembrar? Ele é o princípio básico do modelo de amostragem passiva, ou seja, quanto maior a ilha maior sua capacidade de interceptar propágulos e, portanto, maior sua taxa de imigração. Digamos que a relação entre área da ilha e sua taxa de imigração seja a seguinte:

e = 0 ; f = .01
curve(e+f*x,0,100,bty="l",xlab="Área da ilha",
	 ylab="Taxa de imigração",font.lab=2,lwd=2,ylim=c(0,1))

Tomando-se as já estabelecidas relações entre área e taxa de extinção e distância e taxa de imigração (ver o tópico Adicionando ilhas acima), teremos agora o seguinte conjunto de relações:

par(mfrow=c(1,2))

curve(a+b*x,0,100,bty="l",xlab="Distância da ilha ao continente",ylab="Taxas",
 font.lab=2,lwd=2,ylim=c(0,1),col=4,main="Efeito da distância")
curve(g+h*x,0,100,bty="l",lwd=2,add=T,col=2)

curve(c+d*x,0,100,bty="l",xlab="Área da ilha",ylab="Taxas",
 font.lab=2,lwd=2,ylim=c(0,1),col=2,main="Efeito da área")
curve(g+h*x,0,100,bty="l",lwd=2,add=T,col=4)

Quais as retas representam as taxas de extinção e quais representam as taxas de imigração? Uma dica: lembre-se que azul é a cor do bem e vermelho a cor do mal.

Se juntarmos esses novos efeitos no modelo de equilíbrio de MacArthur & Wilson teremos um modelo mais complicado e com novas propriedades. Quer ver? É só rodar a função abaixo:

# Modelo de equilíbrio 2.0

MW.2.0=function(areas , dist , P , peso.A=.5 , a=1, b=-.01, c=1, d=-.01, e=0, f=.01, g=0, h=.01){
	E=((a+b*areas)*peso.A+(g+h*dist)*(1-peso.A))/(peso.A+(1-peso.A))
	I=((c+d*dist)*peso.A+(e+f*areas)*(1-peso.A))/(peso.A+(1-peso.A))
	S=numeric()
	for(i in 1:length(areas)){S[i]=I[i]*P/(I[i]+E[i])}
	T=numeric()
	for(i in 1:length(areas)){T[i]=I[i]*E[i]/(I[i]+E[i])}

	curve(I[1]-I[1]*x/P,0,P,bty="n",xaxt="n",yaxt="n",xlab="Número de espécies",
	 ylab="Taxas",font.lab=2,lwd=2,ylim=c(0,1),main="Equilíbrio de M&W")
	curve((E[1]/P)*x,0,P,lwd=2,add=T)
	abline(v=0)
	abline(h=0)
	mtext("P",side=1,at=P,font=2)
	mtext("I1",side=2,at=I[1],font=2,las=1)
	mtext("E1",side=4,at=E[1],font=2,las=1)
	mtext("S1",side=1,at=S[1],font=2,col=2)
	mtext("T1",side=2,at=T[1],font=2,las=1,col=2)
	points(S[1],T[1],col=2,pch=16,cex=1.3)
	segments(S[1],T[1],S[1],0,lty=3,col=2)
	segments(S[1],T[1],0,T[1],lty=3,col=2)

	for(i in 2:length(areas)){
		curve(I[i]-I[i]*x/P,0,P,lwd=2,ylim=c(0,1),add=T,lty=i)
		curve((E[i]/P)*x,0,P,lwd=2,add=T,lty=i)
		mtext(paste("I",i,sep=""),side=2,at=I[i],font=2,las=1)
		mtext(paste("E",i,sep=""),side=4,at=E[i],font=2,las=1)
		mtext(paste("S",i,sep=""),side=1,at=S[i],font=2,col=i+1)
		mtext(paste("T",i,sep=""),side=2,at=T[i],font=2,las=1,col=i+1)
		points(S[i],T[i],col=i+1,pch=16,cex=1.3)
		segments(S[i],T[i],S[i],0,lty=3,col=i+1)
		segments(S[i],T[i],0,T[i],lty=3,col=i+1)
		}

	ex=data.frame(areas=areas,spp=S,dist=dist)
	y=lm(S~areas)[[1]][1]
	z=lm(S~areas)[[1]][2]

	plot(spp~areas,data=ex,log="xy",font.lab=2,pch=16,col=2,bty="l",
	 main=c("Relação espécies-área",paste("c = ",round(y,2),"; z = ",round(z,2))),
	 xlab="Área da ilha",ylab="Número de espécies",ylim=c(1,P))
	abline(lm(log10(spp)~log10(areas),data=ex),lty=3)

	return(ex)
	}

Note que foi preciso acrescentar mais quatro parâmetros à nossa função: e, f, g e h, que correspondem às relações entre área e imigração e entre distância e extinção, respectivamente. Note também que foi preciso estabelecer uma ordem de importância entre os fatores distância e área. Por exemplo, sabendo que a imigração aumenta com a área da ilha, mas diminui com a distância desta ilha ao continente, a taxa de imigração em uma ilha pequena próxima do continente deve ser maior do que a taxa de imigração em uma ilha grande, porém distante do continente? Foi para responder a essa pergunta que criamos o argumento peso.A na função. peso.A se refere à importância da área em relação à distância. Portanto, se peso.A=1, a distância não terá importância alguma, se peso.A=0, então só a distância tem importância, e se peso.A=.5, distância e área terão a mesma importância.

Infelizmente, não teremos tempo para fazermos todas as combinações de parâmetros que gostaríamos em aula, por isso adiantamos algumas para você:

# Ilhas com diferentes áreas, mas com as mesmas distâncias
par(mfrow=c(1,2))
MW.2.0(areas=c(1,15,30,60,90) , dist=rep(50,5) , P=100, peso.A=.5)

# Ilhas com as mesmas áreas, mas com diferentes distâncias
MW.2.0(areas=rep(50,5) , dist=c(1,15,30,60,90) , P=100, peso.A=.5)

# Ilhas com diferentes áreas e distâncias
MW.2.0(areas=c(1,15,30,60,90) , dist=c(90,60,30,15,1) , P=100, peso.A=.5)
MW.2.0(areas=c(1,15,30,60,90) , dist=c(1,15,30,60,90) , P=100, peso.A=.5)
MW.2.0(areas=c(1,10,15,30,45) , dist=c(2,20,30,60,90) , P=100, peso.A=.5)

Vamos agora comparar esse novo modelo 2.0 ao original:

# Comparando...
MW(areas=c(1,15,30,60,90) , dist=rep(50,5) , P=100)
x11()
par(mfrow=c(1,2))
MW.2.0(areas=c(1,15,30,60,90) , dist=rep(50,5) , P=100, peso.A=.5)

MW(areas=rep(50,5) , dist=c(1,15,30,60,90) , P=100)
x11()
par(mfrow=c(1,2))
MW.2.0(areas=rep(50,5) , dist=c(1,15,30,60,90) , P=100, peso.A=.5)

MW(areas=c(1,15,30,60,90) , dist=c(90,60,30,15,1) , P=100)
x11()
par(mfrow=c(1,2))
MW.2.0(areas=c(1,15,30,60,90) , dist=c(90,60,30,15,1) , P=100, peso.A=.5)

MW(areas=c(1,15,30,60,90) , dist=c(1,15,30,60,90) , P=100)
x11()
par(mfrow=c(1,2))
MW.2.0(areas=c(1,15,30,60,90) , dist=c(1,15,30,60,90) , P=100, peso.A=.5)

MW(areas=c(1,10,15,30,45) , dist=c(2,20,30,60,90) , P=100)
x11()
par(mfrow=c(1,2))
MW.2.0(areas=c(1,10,15,30,45) , dist=c(2,20,30,60,90) , P=100, peso.A=.5)

# Comparando II (alterando peso.A)
par(mfrow=c(2,2))
MW.2.0(areas=c(1,15,30,60,90) , dist=rep(50,5) , P=100, peso.A=1)
MW.2.0(areas=c(1,15,30,60,90) , dist=rep(50,5) , P=100, peso.A=.5)

Entre um modelo e outro houve alteração do resultado? Essa mudança foi qualitativa ou quantitativa? É alterado somente o número de espécies em equilíbrio (S) ou também a taxa de substituição (T)?

Uma das primeiras explicações para a relação espécies-área foi a de que quanto maior uma ilha, mais tipos diferentes de habitats ela abrigava. Assim, quanto maior a ilha, maior a diversidade de habitats e, portanto, maior o número de espécies. Note que para isso ser verdade cada espécie só deve ser capaz de viver em determinado tipo de habitat. Acontece que isso raramente é encontrado na natureza e é por essas e outras que essa hipótese anda em baixa hoje em dia. Em todo caso vamos dar uma olhadinha nela.

Primeiro vamos modelar um sistema em que cada espécie só pode viver em um determinado tipo de habitat e cada habitat só pode abrigar um tipo de espécie. Antes de seguirmos em frente é preciso determinarmos qual a relação entre área da ilha e a quantidade de habitats ela tem:

a=0 ; b=1.5
area=c(5,10,20,50)

hab.ilha=round(a+b*area)

riq=hab.ilha

mod=lm(log10(riq)~log10(area))
mod

plot(riq~area,log="xy",main=c("Um habitat, uma espécie",
 paste("c = ",round(mod[[1]][1],2),"; z = ",round(mod[[1]][2],2))),bty="l",font.lab=2)
abline(mod,col=2)

Viu como esse modelo é simples? Mas não se deixe levar pelas aparências. Apesar de ele ser de longe o mais simples, é também o que precisa de mais premissas difíceis de aceitar. Lembra quais são?

Este modelo depende somente de uma coisa. Veja se consegue descobrir usando a função abaixo e variando os parâmetros desta função.

uma.sp.um.hab=function(area , a , b){
	riq=round(a+b*area)
	mod=lm(log10(riq)~log10(area))
	plot(riq~area,log="xy",xlab="Área",ylab="Número de espécies",main=c("Um habitat, uma espécie",
	 paste("c = ",round(mod[[1]][1],2),"; z = ",round(mod[[1]][2],2))),bty="l",font.lab=2)
	abline(mod,col=2)
	res=data.frame(area=area,riqueza=riq)
	return(res)
	}

uma.sp.um.hab(area=1:100, a=10, b=2)

Imaginemos agora que os habitats ocorrem ao acaso nas ilhas. Então, quanto maior a ilha, maior a chance de haver maior quantidades de habitats diferentes (maior diversidade de habitats).

Nhab=100
hab=paste("habitat",1:Nhab)
hab.spp=1 # relação número de habitats / número de espécies
Nspp=Nhab/hab.spp
hab.area=1 # relação entre área e número de habtats
area=c(1,10,20,50,90)
hab.ilha=area/hab.area
prop.hab=rep(1,100)
riq=numeric()
for(i in 1:length(area)){
	riq[i]=length(unique(sample(hab,hab.ilha[i],replace=T,prob=prop.hab)))
	}
plot(riq~area,log="xy")
abline(lm(log10(riq)~log10(area)),col=2)

• Gotelli, N.J. 2007 Ecologia. Cap. 7 - Biogeografia de ilhas. Pp. 159-181. Ed. Planta.

Script