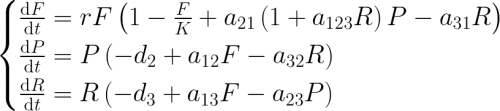Southern-Summer School on Mathematical Biology

In nature, ecosystems are full of ecological interactions. The ecological interactions could occur between two or more species and will be an interchange of services or resources between them. The outcome of ecological interactions can be positive, neutral or negative for each of the involved species. The combination of the outcome for each species is how we classify the type of ecological interaction. For instance, mutualism are interactions in which all interacting partners benefit from the interaction like seed dispersal and others. But, when one species benefit, as a predator, and the other species has a loss, as the prey, this is an antagonism.

Pollination is usually considered a mutualistic interaction. The reason is that most plants need to transfer pollen from its own flowers to other's individuals flowers to successfully reproduce, and the animals do this in the pollination process. On the other hand, animals benefit from eating part of the pollen or nectar that they acquire while interacting. In this scenario, both the flower and the pollinator gain from the pollination process. However, relationships can be more complicated; interactions do not happen in isolation. Some animals can cheat, acquiring the resources from flowers by alternative ways. Some bees, for example, are able to cut a hole in the side of the flower large enough to access the nectar (nectar robbers, as shown in the figure).

The presence of nectar robbers in plant-pollinator interactions hamper our understanding of the interaction. Even though robbers will always benefit from the interaction, plants and pollinators could be positively, negatively or remain unaffected by interacting with robbers. Nectar robbers could be costly to plants as they obtain pollen and nectar without providing pollination. Moreover, nectar robbers could damage ovary or other structures of the flowers not allowing reproduction, or could else interact aggressively with the pollinators, startling them, or even make the robbed flowers unattractive to pollinators. However, some studies point out that we may not be catching all plant-pollinator-robber dynamics. Zhang et al (2007) proposed that nectar robbing could indirectly affect plant reproduction, by changing pollinators' behavior or frequency of visitation, bringing even positive consequences for the plants. If the presence of robbed flowers changes pollinators behavior, making pollinators visit more flowers, it could improve pollen flow and out-crossing. Varma & Sino (2019) observed that the behaviour of the pollinator could change because of the presence of cheaters, indicating a higher foraging efficiency of pollinators.

The interplay between distinct interacting partners could elucidate the underlying mechanism that regulates interaction species dynamics. Build a mathematical model with the mechanisms that could modulate plant-pollinator-robber interactions to enables us to deepen our knowledge about the interaction dynamics.

• How could the population proportions of each group (pollinator, plants, robbers) or even the interaction frequencies modulate the persistence and dynamics of the interaction?

• In which scenarios robbers could act as mutualistic or as antagonistic partners to plant-pollinators?

Further well-grounded questions from the group are welcome.

Varma & Sino, 2019. Nectar robbing in bellflower (Sesamum radiatum) benefited pollinators but an unaffected maternal function of plant reproduction

Zhang et al 2007. Effects of nectar-robbing on plant reproduction and evolution

We will model a network with 3 species interacting with 3 ecological processes:

- Mutualism between the plant and the pollinator

- Predation of the robbers in the flowers

- Competition by interference between pollinators and robbers for nectar

DESCRIPTION OF THE SYSTEM

PLANTS-FLOWERS

- Dioecious: both male and female organs in the same flower

- Obligate outcrossing mating strategy: the flower must be pollinated by pollen from another flower, and it must be done by an animal visiting.

- Pollination is specialized, i.e. done by one species of animal.

- We will model the population of flowers instead of plants, i.e., considering one flower per plant.

- The plant has negligible costs in producing more nectar when it is depleted by the visitors (pollinators and nectar robbers)

- The production of nectar is proportional to the number of flowers

POLLINATORS

- Specialized in the species of plant. The population can only grow with nectar consumption in the system.

- It can die “naturally” by other causes in a constant rate.

- It has the behavior to increase the flower visit rates (and pollination) in searching for nectar when the amount of nectar per flower is low. But it has no cost for increasing the visitation rate.

- It doesn't know how much nectar there is in the flower, so the pollinators can visit and pollinate the flower even though it has no nectar.

- Pollinator growth rate related to nectar consumption has a saturation point, in which even though the nectar amount increases the number of pollinators does not increase anymore.

NECTAR ROBBERS

- Generalist species. They can robber nectar from other plants out of our system, but it is limited by a carrying capacity in the environment.

- It consumes nectar from the flower competing by interference with the pollinators by nectar resources

- Robbers don't know how much nectar there is in the flower, so it opens holes in flowers regardless of the amount of nectar. They damage (kill) flowers independently of the nectar amount.

- Robbers' growth rate related to nectar consumption has a saturation point, in which even though the nectar amount increases the number of robbers does not increase anymore.

Let F be the population of flowers, N the amount of nectar available, P the population of pollinators and R the population of nectar robbers.

We assume in our model:

- The pollinators and the flowers have a mutualistic interaction:

1. The flowers benefit from pollinator's visit for nectar - it increases flower growth rate.
2. The pollinator eats flower nectar and increases its population size.
3. The pollinators can't survive without flowers

- The robbers and the flowers have a predator-prey-like interaction.

1. The robbers eat nectar and damage the flower
2. The robbers can't survive without flowers
3. The robbers will not increase linearly as the number of flowers increases because it saturates, i.e. robbers can not eat as much as flower there are available

- The robbers and the pollinators compete for the nectar.

1. The robbers can force the pollinators to change their behavior, making them increase their outcrossing rate and visit more flowers due to nectar scarcity. This is beneficial to the flower population.

With these assumptions, we proposed

All parameters are non-negative. K is the carrying capacity of the flowers purely through self-pollination.

In this model, the resource the robbers and pollinators compete for, nectar, is taken into account implicitly. The immediate problems we saw with the model were

• No account of the nectar dynamics. In fact, in this model competition persists independently of the population of flowers.
• The indefinite linear growth of the benefit to the flower in the number of robbers via a ternary interaction is unrealistic.

We have the following fixed points:

Code in R

Code in Python