Estocasticidade Demográfica

Neste exercício vamos projetar o crescimento exponencial em tempo discreto de duas formas diferentes: sem estocasticidade demográfica(determinístico) e com estocasticidade demográfica.

Ao contrário do exercício anterior onde usamos os parâmetros de crescimento populacional (r e lambda), neste vamos modelar diretamente os eventos de reprodução (b) e mortalidade (d) para projetar as populações. Ou seja, iremos usar as taxas b e d para estimar quantos indivíduos nascem e quantos morrem em cada passo no tempo.

Na primeira parte faremos isso de forma determinística, onde os valores b e d determinam o crescimento da população e são constantes. Na segunda parte cada indivíduo poderá morrer ou reproduzir dada uma probabilidade, como se fosse lançada uma moeda para determinar a sua sobrevivência ou reprodução. Esta forma de modelar o crescimento da população vai evidenciar a impossibilidade dos indivíduos poderem sobreviver ou reproduzir em frações.

Por fim, iremos fazer um gráfico que mostra o crescimento determinístico e o crescimento estocástico, para que possamos compará-los. Olhe também os valores apresentados no final da execução da função e note como a diferença entre taxa base e taxa realizada varia com o tamanho da população, tanto para b como para d.
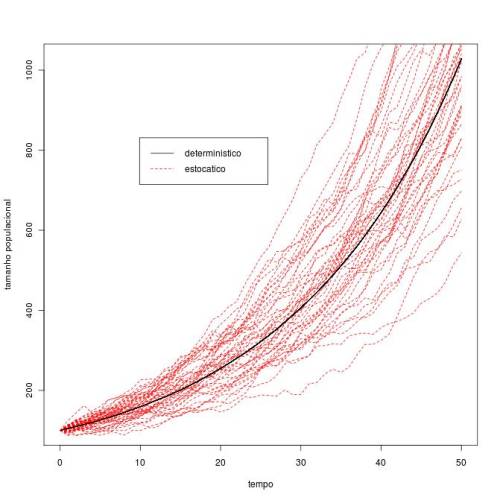
Testar com b=0.14, d=0.08, No = 100, tmax= 50
<box 70 red |Uma função pronta> Veja uma solução para o código da função aqui: estoc_demog.r </box>

• 1. determine quais os argumentos da função:

 est.dem=function(N0=100, b=0.55, d=0.5, tmax=50)
{
...
}

• 2. crie o objeto para armazenar os resultados da projeção das populações: uma tabela com sete colunas preenchidas com zeros e os respectivos nomes das colunas

 est.dem=function(N0=100, b=0.55, d=0.5, tmax=50)
{
resulta=matrix(0,ncol=7, nrow=(tmax+1))
colnames(resulta)=c("tempo", "Nt.st", "nasc.st", "mort.st", "Nt.dt", "nasc.dt", "mort.dt")
...

• 3. Preparando os dados inciais:
  • 3.1. Colocar o valor de tempo na primeira coluna
  • 3.2. O tamanho inicial (N0) na primeira linha da segunda e quinta colunas
  • 3.3. Calcular as probabilidades de morte e nascimento (Gotelli, 2007: Eq.1.10 e 1.11)
    

est.dem=function(N0=100, b=0.55, d=0.5, tmax=50)
{
resulta=matrix(0,ncol=7, nrow=(tmax+1))
colnames(resulta)=c("tempo", "Nt.dt", "nasc.dt", "mort.dt", "Nt.st", "nasc.st", "mort.st")
resulta[,1]=0:tmax
resulta[1,c(2,5)]=N0
pnasc=b/(b+d)
pmort=d/(b+d)
...

• 4. Criar um ciclo para os cálculos das projeções:
  • 4.1. Salve o tamanho populacional no tempo anterior para as duas projeções

...
  for(t in 2:(tmax+1))
  {
  nt.st=resulta[(t-1),2]
  nt.dt=resulta[(t-1),5]
...
  }
...

• 5. Calcule a projeção para o modelo determinístico
  • 5.1. Antes de inciar os cálculos garanta que o nt.dt é maior que ZERO, pois se a população se extinguiu não há o que projetar.

...
if(nt.dt>0)
{
...
}
...

• 5.2. Dentro do condicionante if:
  • Calcule o número de mortes (d * nt.dt), chame de n.mort.dt
  • Calcule o número de nascimentos (b * nt.dt), chame de n.nasc.dt
  • Guarde esses valores na matriz resultado
  • Calcule o tamanho populacional no tempo t+1 que será igual ao N anterior mais os nascimentos menos as mortes (nt.dt1 = nt.dt + n.nasc.dt - n.mort.dt)
• 5.3. Crie outro condicionante para saber se o nt1.dt > 0 . Caso verdadeiro, coloque o valor correspondente na matriz resultado (isso evita colocarmos valores de populações negativas no resultado)

• 6. Vamos calcular agora os valores para a projeção estocástica:
  • 6.1. Primeiro criamos o condicionante para saber se a população não extinguiu da mesma forma que para o modelo determinístico
  • 6.2. Calculamos o número de mortes e nascimentos pela probabilidade de nascimento e mortalidade que calculamos no início da função (tópico 3.3). Para gerar o número de eventos de mortalidade e nascimento em função da probabilidade utilizamos a função rbinom. Essa função cria valores aleatórios de número de sucessos (aqui natalidade ou morte) a partir do número de tentativas (no caso o número de indivíduos da população), veja o help do R para maiores informações.

...
n.nasc.st=rbinom(1,nt.st,pnasc)
n.mort.st=rbinom(1,nt.st,pmort)
...

• 7. Complete a função com os mesmos passos do modelo determinístico, terminando com o comando para retornar a matriz resultado e fechando a função.

...
return(resulta)
}

Confira se todos os parênteses e colchetes estão corretamente colocados

• 8. Rode a função com os parâmetros padrão (N0=100, b=0.55, d=0.5, tmax=50) e produza o gráfico com os valores das projeções por tempo:

estima=est.dem(N0=100, b=0.55, d=0.5, tmax=50)
plot(estima[,1], estima[,2], type="l",xlab="tempo", ylab="tamanho populacional")
points(estima[,1], estima[,5], type="l", col=2, lty=2)
legend(locator(1),legend=c("deterministico", "estocatico"), lty=c(1,2), col=c(1,2))

• 9.Faça isso várias vezes e a cada vez inclua no gráfico anterior a projeção estocástica e determinística. Rode os códigos abaixo várias vezes, como a função points é subordinada ao plot, as linhas de projeção serão incluídas no gráfico anterior.

estima=est.dem(N0=100, b=0.55, d=0.5, tmax=50)
points(estima[,1], estima[,2], type="l")
points(estima[,1], estima[,5], type="l", col=2, lty=2)

• 10. Varie o valor inicial da população (N0=10) e produza os gráfico novamente com muitas simulações.
  • 10.1. Há alguma chance de haver extinção no modelo determinístico?
  • 10.2. E no estocástico?
  • 10.3. Caso haja possibilidade de extinção, é possível calcular a probabilidade?
• 11. Varie a mortalidade e a natalidade para que a população cresça ou decresça mais ou menos rapidamente.

• 12. Estime a variação de b e d em populações com N0s diferentes e parâmetros iguais.
  • 12.1. Rode o script abaixo variando os valores de N0 e interprete os gráficos produzidos.

par(mfrow=c(1,2))
estima10=est.dem(N0=10, b=0.55, d=0.5, tmax=50)
nt=dim(estima10)[1]-1
plot(estima10[1:nt,"tempo"], estima10[1:nt,"b.dt"],
ylim=c(0,max(estima10[,c(5,6,10,11)])),xlab="tempo", ylab="taxas")
points(estima10[1:nt,"tempo"], estima10[1:nt,"d.dt"], col="red") 
lines(estima10[1:nt,"tempo"], estima10[1:nt,"d.st"], col="red")
lines(estima10[1:nt,"tempo"], estima10[1:nt,"b.st"])
legend(locator(1), legend=c("b.base", "d.base","b.realizado", "d.realizado"),pch=c(1,1,NA,NA),
lty=c(NA,NA,1,2),col=c(1,2,1,2))

estima100=est.dem(N0=100, b=0.55, d=0.5, tmax=50)
nt=dim(estima100)[1]-1
plot(estima100[1:nt,"tempo"], estima100[1:nt,"b.dt"],
ylim=c(0,max(estima100[,c(5,6,10,11)])),xlab="tempo", ylab="taxas")
points(estima100[1:nt,"tempo"], estima100[1:nt,"d.dt"], col="red") 
lines(estima100[1:nt,"tempo"], estima100[1:nt,"d.st"], col="red")
lines(estima100[1:nt,"tempo"], estima100[1:nt,"b.st"])
legend(locator(1), legend=c("b.base", "d.base","b.realizado", "d.realizado"),pch=c(1,1,NA,NA),
lty=c(NA,NA,1,2),col=c(1,2,1,2))