I) DERIVADA

A derivada de uma função é uma operação que fornece a taxa de variação instantânea desta função. Esta taxa é calculada para cada valor no domínio da função e representa a variação do valor da função quando se considera um intervalo de variação da variável de interesse tendendo a 0. Isso fica mais claro simbolicamente. Consideremos uma variável qualquer $x$ e uma função dessa variável $f(x)$. A derivada de $f(x)$ será:

$$ \lim\limits_{\Delta x \to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}$$

A qual é representada por

• $ f'(x)$ ou $\frac{d}{dx}f(x)$

A derivada também pode ser definida geometricamente, como a tangente do ângulo $\theta$ em relação ao eixo da variável ($x$). Este ângulo é formado pela semi reta que liga o ponto $x$ a um outro ponto de $f(x)$ infinitesimalmente próximo a ele. Ou seja,

$$ f'(x)= \frac{d}{dx}f(x)=\lim\limits_{\Delta x \to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}=tg(\theta)$$

Existem algumas poucas regras de derivação que facilitam o cálculo da derivada da grande maioria das funções. Essas regras, expostas em aula, serão usadas para o cálculo das derivadas abaixo.

$f(x)=g(x)+h(x)$
$f'(x)=g'(x)+h'(x)$

$f(x)=g(x)+h(x)$
$f'(x)=g'(x)+h'(x)$

$f'(x)=g'(x)+h'(x)$
$f'(x)=-sin(x)+cos(x)

$f(x)=g(x)+h(x)j(x)$
$f'(x)=g'(x)+h'(x)j(x)+h(x)j'(x)$ $f'(x)=2x+3x^2cos(x)-sin(x)x^3$

$f(x)=g(x)h(x)$
$f'(x)=g'(x)h(x)+g(x)h'(x)$ $f'(x)=exp(x)ln(x)+\frac{exp(x)}{x}$

$f'(x)=g'(x)+h'(x)$ $f'(x)=5x^4sin(x)+x^5cos(x)$

$f(x)=\frac{g(x)}{h(x)}$
$f'(x)=\frac{g'(x)h(x)-g(x)h'(x)}{h(x)^2}$

$f'(x)=\frac{g'(x)h(x)-g(x)h'(x)}{h(x)^2}$

$f'(x)=\frac{exp(x)x-exp(x)}{x^2}$

$f'(x)=\frac{cos(x)x^2-2xsin(x)}{x⁴}$

Derivadas.wxm

Graficos

Codigo em R para os gráficos

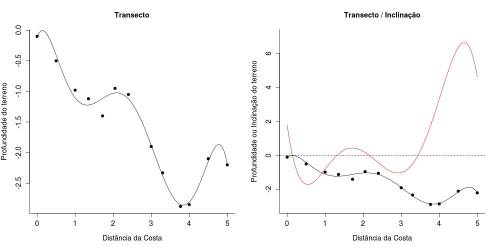
• 1) A função da inclinação do terreno pode ser obtida derivando-se a profundidade do terreno em função da distância da costa. A partir de um modelo linear multiplo (polinomial de sexta ordem; não sei se esta terminologia está correta…) e dos pontos de profundidade e distancia coletados, estimou-se como seria o perfil do terreno até 5km da costa.
  

Este modelo do perfil do terreno é descrito pela função de sexto grau abaixo $PR(d)$,

$$ PR(d) = -0.042d^6+0.619d^5-3.315d^4+7.906d^3-7.951d^2+1.799d-0.119$$ Portanto, a inclinação do terreno $I(d)$ em função da distância da costa será,

$$ I(d) = \frac{d}{dt}PR(d)= -0.252d^5+3.095d^4-13.26d^3+23.718d^2-15.902d+1.799$$ O que pode ser conferido em Inclinacao.wxm

• 2) Os gráficos da profundidade e da inclinação do terreno são apresentados abaixo. Entretanto, parece-me que há um erro aqui, o qual não consegui resolver. Se assumirmos que o gráfico da função $PR(d)$ está correto, eu esperaria que sua derivada fosse nula ($I(d)= 0$) em algum ponto nas proximidades de $d = 4$ ou de $d = 5$. Porém isso não ocorre.
  

Este problema está ocorrendo no R quando se manda plotar o gráfico de $PR(d)$. Ao plotar os gráficos de $PR(d)$ e de $I(d)$ no Maxima percebemos que o gráfico da inclinação está similar ao seu correspondente em R. Porém o gráfico do perfil do terreno está diferente. O gráfico do R se ajusta melhor aos pontos porém, no Maxima, o gráfico do terreno é mais coerente com o gráfico da inclinação.

Verfiquei se a função estava errada ou se a plotagem usando o predict do modelo coincidia com o da minha função, e esse não foi o problema. De todo mode, com base nesses gŕaficos algumas relações podem ser estabelecidas. Primeiro é que em média. Isso poderia ser verificado encontrando-se a média das inclinações no intervalo de distância considerado. Ou seja, calcula-se a integral de $I(d)$ definida nos pontos de observação e divide-se o resultado dessa operação por $\Delta d$. Se o resultado de toda essa operação for menor que 0, sabemos que a tendência é do terreno se tornar mais profundo conforme percorremos o terreno da costa para o mar.

$$ \frac{\int _0^5 I(d)dd}{\Delta d }= \frac{\int _0^5 I(d)dd}{5}<0$$

Entretanto, o terreno é irregular, ou seja a inclinação não é constante ao longo do tempo, mas varia não linearmente, com momentos em que cresce ao longo de $d$ e momentos em que decresce. Isso implica que há “vales” e “topos” no gráfico do perfil do terreno, sendo que no ponto mais baixo de um “vale” e no pontos mais alto de um “topo” $I(d)=0$. Isso se convencionou chamar de máximos e mínimos locais. Para saber se um ponto em que $I(d)=0$ serefere a um máximo ou mínimo local, deve-se calcular a segunda derivada de $PR(d)$. O ponto será um mínimo local se

$$ \frac{\delta^2}{\delta d^2}PR(d)>0$$

Por lado, o ponto será de máximo local se

$$ \frac{\delta^2}{\delta d^2}PR(d)<0$$

Por fim, vale ressaltar que quanto mais profundo o terreno, menos luz ele receberá. Além disso, dado que o sol nasce em leste, as faces voltadas para oeste estarão mais sombreadas ao longo do dia pelo formato do relevo. Então, dada uma certa profundidade, as faces voltadas para leste receberão mais luz solar em comparação com as faces oeste de terreno. As faces leste correspondem a pontos do terreno cuja inclinação é negativa, enquanto que inclinações positivas definem as faces leste.

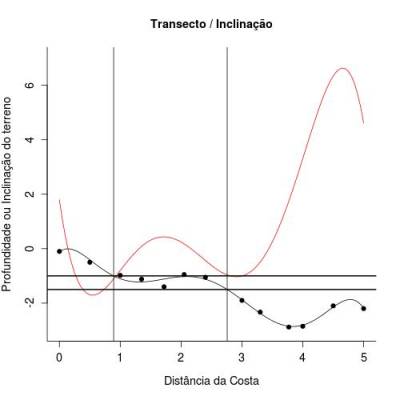
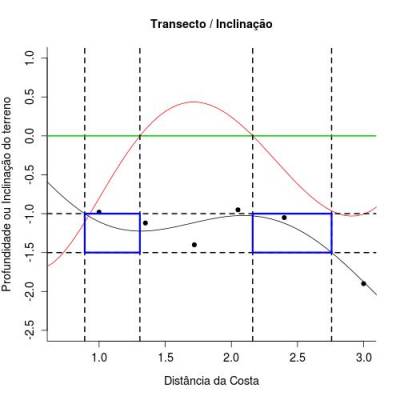
• 3) Espero encontrar mais baleias em locais entre 1 e 5km da costa e com inclinação negativa do terreno (fig.1). Infelizmente não consegui calcular desigualdades no Maxima, tampouco achar a solução de equações polinomiais de graus elevados. No entanto não olhei o deSolve para R. Desta forma, representei essa localização aproximadamente na figura abaixo. A base dos quadrilateros azuis (fig.2) indica a faixa de distância em que se espera encontrar a maior proporção de baleias. Estes valores foram estimados nas faixas entre 0.89 - 1.31 e 2.16 - 2.76 $km$ da costa.
  

Dentre outras coisas esse padrão pode ser explicado pela descrição apresentada na resposta anterior. Nesta faixa, a profundidade ainda não é tão grande a ponto de inibir completamente a chegada de luz, assim como locais do terreno voltados para face leste nesta região receberão mais luz que terrenos voltados para oeste. Nesses locais, espera-se, dentre outras coisas, que a produtividade primaria seja mais elevada e que, portanto, as baleias encontrarão mais recursos alimentares nesta faixa.

Codigos em R do Exercício 2!!!