IV) MODELOS DE DINÂMICA DE POPULAÇÕES INDEPENDENTES DE DENSIDADE

Eu não entendi muito bem a técnica de força bruta para a transformação da equação de crescimento discreto para crescimento continuo. De fato, compreendi o mecanismo de se procurar o limite em que o tempo entre gerações tenda a zero ou o número de gerações por unidade de tempo continuo tenda ao infinito ($\Delta t \to 0$ ou $n \to \infty$). Porém, não captei como esse limite foi calculado (no caso, para $n \to \infty$).

O exemplo apresentado no roteiro me pareceu mais uma dessas inspirações sobrenaturais. O que percebi é que se acha um número, portanto trata-se de uma solução numérica. Mas daí só com muita inspiração para inferir que o valor encontrado é $e^r$. Na verdade, para alguns casos particulares como quando o resultado é $e^r$ ou algo linear a inspiração não precisa ser muito grande. Mas para muitos outros casos, isso não é tão intuitivo. Se estou correto, isso torna essa técnica muito restrita ( mas, se possível, gostaria de saber mais detalhes de como se calcula analiticamente o limite acima ).

Lembrei-me de uma técnica que vi em alguns livros. Ela me parece mais lógica, mas não sei o quão geral ela é. Considerando o modelo de crescimento apresentado, trata-se de se fazer as seguintes operações:

$ N_{t+1}=\lambda N_t$

Subtraindo $N_t$ e dividindo por $\Delta t$ dos dois lados da equação teremos:

$ \frac{N_{t+1}-N_t}{\Delta t}=\frac{N_t\lambda-N_t}{\Delta t}=\frac{N_t(\lambda-1)}{\Delta t}$

Se considerarmos esta equação acima num limite em que $\Delta t \to 0$, o primeiro termo da equação será igual a $\frac{d}{dt}N_t$. Então:

$ \frac{d}{dt}N_t = (1-\lambda)Nt$. Uma vez que $1-\lambda =r$, essa equação diferencial será:

$ \frac{d}{dt}N_t = rNt$, cuja solução é:

$ N_t = ce^{rt}$. Sendo $c$ o intercepto da função, $c = N_0$. Assim, $$N_t = N_0e^{rt}$$

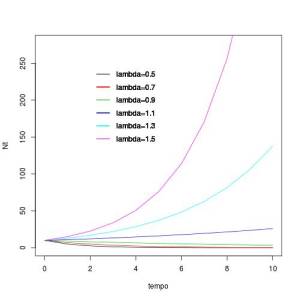
• 1) Ao se projetar as populações com diferentes lambdas, dois padrões são facilmente observáveis. Primeiro é que se o $0<\lambda<1$ a população diminui de tamanho com o tempo e se $\lambda > 1$ a população aumenta com o tempo. Isso se deve ao fato da taxa de crescimento individual($r$) variar teóricamente entre -1 e $\infty$ (pois não é possível termos uma taxa de mortalidade individual $d >1$ individuo / individuo.tempo). Lembrando que $r = \lambda-1 = b-d$, em que $b$, $d>0$.

Segundo, é que para $\lambda > 1$, quanto for o $\lambda$, mas rápido é o crescimento populacional com o tempo. Ao contrário, para $0<\lambda < 1$, quanto mais próximo de 0 for $\lambda$, mais rápido é o declínio do tamanho populacional com o tempo. Por fim, vale enfatizar que as população crescerão indefinidamente ($\lambda > 1$) ou se extinguirão ($0<\lambda < 1$) com o tempo.

• 2)

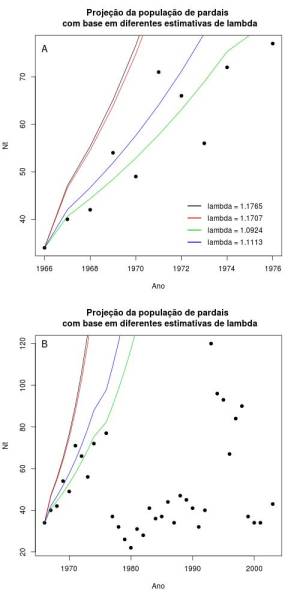
Neste exercício, considerei a estimativa de $\lambda$ como sendo a média aritmética dos $\lambda$s calculados para o intervalo entre cada geração. Pode-se perceber que quanto maior for número de gerações usado para o cálculo da estimativa de $\lambda$, mais precisa será esta estimativa. Na realidade, as estimativas para número de gerações baixos (i.e. 2 ou 4) são muito pouco precisas se considerarmos uma análise para um intervalo de tempo total de 10 anos (fig.1). De fato, 8 gerações parece fornecer uma boa estimativa de $\lambda$, sendo que o uso de 10 gerações desviou um pouco mais, mas ainda permanece uma estimativa apropriada (fig.1).

Entretanto, se usássemos quaisquer destes valores para prever o tamanho populacional de pardais nos 36 anos amostrados, perceberíamos que nenhuma das estimativas é apropriada. Na realidade, este modelo de crescimento populacional exponencial se mostraria inadequado (e na verdade ele sempre será para populações em condições naturais), visto que a população de pardais não cresceu indefinidamente ao longo do tempo. Ela na realidade parece oscilar (fig.2).

$ N_t= N_0e^{rt}$

$ 2N_0=N_0e^{rt}$

$ 2 = e^{rt}$

$ln(2) = rt$
$$t_{duplic} =\frac{ln(2)}{r}$$

A função em R é:

t.duplic<-function(r) log(2)/r

rs<-c(0.01,0.1,0.5,1)
resp.ex3<-t.duplic(rs)
resp.ex3

Gerando os seguintes resultados:

$t_{duplic}|r=0.01 = 69.31$

$t_{duplic}|r=0.1 = 6.93$

$t_{duplic}|r=0.5 = 1.39$

$t_{duplic}|r=1 = 0.69$

• Preço total
  1. Opção 1 = R$ 81.112,48
  2. Opção 2 = R$ 43.991,09
• Valor das prestações
  1. R$ 811,12
  2. R$ 879,82
• Quantos carros a mais estarei pagando
  1. 3 carros
  2. 1,42 carros
• Tempo de duplicação do valor dos carros
  1. 63,01 meses ou 5.25 anos
  2. 99,02 meses ou 8.25 anos
• Pagar mais caro é inevitável quando se compra em prestações com juros. Na melhor das hipóteses pagamos quase 1,5 vezes o valor original do carro. Entretanto a segunda opção é mais vantajosa, pois apesar do valor inicial ser maior e de se pagar prestações um pouco maiores, paga-se menos pelo carro. O tempo de duplicação do valor do carro é maior que na opção 2.
  

• Neste exercicio, simulei para as condições iniciais: $N0 = 10$, $\hat r = 0.3$ e $\sigma_{\hat r} = 0.01, $t_max 0.06, 0.12, 0.17, 0.23, 0.28, 0.34, 0.39, 0.45, 0.50$. Repeti cada simulação para 10 e para 1000 realizações ( Código em R).
  

Para 10 realizações (pontos = média $Nt$, barras = +/- 1 desvio padrão)


Para 1000 realizações (pontos = média $Nt$, barras = +/- 1 desvio padrão)

• Como podemos perceber, essa afirmação não está correta se houver estocasticidade ambiental. Considerando que a taxa de crescimento ($r$) varia ao longo do tempo de acordo com uma distribuição normal, quanto maior for o desvio padrão de $r$ mais incerta será a predição do tamanho populacional em qualquer $t$. Além disso, o desvio padrão do tamanho populacional aumenta com o tempo, indicando que há uma probabilidade da população se extinguir em qualquer tempo. Esta probabilidade aumenta com o passar do tempo e será tão maior para um dado tempo $t$, quanto maior for o desvio padrão de $r$.
  

Um outro padrão interessante é que a média (e consequentemente o desvio padrão) de $Nt$ será pior estimada quanto menor for o número de realizações (i.e. réplicas) de cada simulação. O que se espera é que a média do tamanho populacional num tempo qualquer seja igual à média esperada pelo modelo determinístico. Em outras palavras, como a média de $r$ é igual ao $r$ do modelo determinístico, depois de muitas simulações, a média de $r$ e portanto de $Nt$ serão iguais às do modelo determinístico. Se o número de realizações da simulação for pequeno, teremos um outro erro associado à estimativa dos parâmetros.