Ordenação

Ordenação é um método de re-descrição dos dados multivariados de forma a apresentá-los em poucas dimensões, geralmente 2 ou 3, com minima perda de informação. Veja o exemplo da representação gráfica de duas amostras em um espaço dimensional de duas esp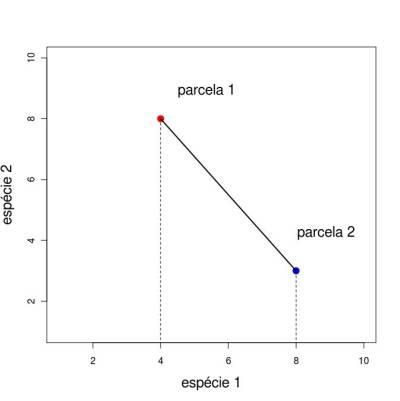écies. Quando temos apenas duas dimensões de atributos (no caso duas espécies) a representação gráfica dos objetos, no nosso caso as parcelas, é direta. Vamos reapresentar nossa comunidade pelas duas primeiras espécies:

sp2=com1.cont[c(1,2),]
duas.sp=sp2[,apply(sp2,2,sum)>0]
plot(t(duas.sp), pch=20, col=rainbow(dim(duas.sp)[2]), xlab="sp1", ylab="sp2")
text(duas.sp[1,]+0.1, duas.sp[2,]+0.4, colnames(duas.sp),col=rainbow(dim(duas.sp)[2]) )

Conforme vamos acrescentando informações de novos atributos (espécies) aos nossos objetos (parcelas), a representação gráfica torna-se mais difícil. Com três dimensões ainda conseguimos representar nossas parcelas em um gráfico. 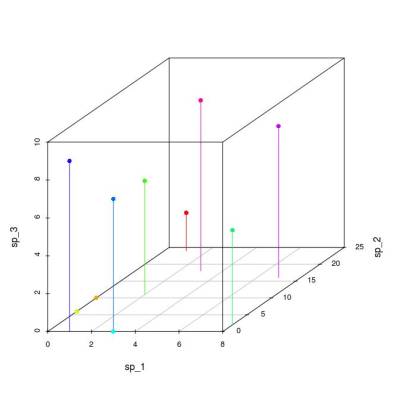Os muitos métodos de ordenação como Análise de Componentes Principais (PCA), Análise de Correspondência (CA), tem como base a redução das dimensões descritivas para melhor visualizar as relações entre os objetos.

Foi um dos primeiros métodos de ordenação e devido a sua simplicidade foi amplamente usado por ecólogos. Apesar de suas limitações e de ter sido preterido por outros métodos mais sofisticados, a Ordenação Polar (OP) produz resultados com interpretação ecologica relevante. O objetivo da OP é representar as parcelas em um sistema de coordenadas de forma que a distância entre as parcelas representem suas similaridades e que revelem o gradiente ambiental subjacente. Aqui vamos usar o algorítmo de OP desenvolvido por Bray e Curtis (1957), especificamente para a análise de dados de comunidades de plantas. Para inciar a análise, primeiro calculamos a dissimilaridade de Bray-Curtis como nossa medida de distânca. Abaixo a modificação da função que usamos para a similaridade, agora calculando a dissimilaridade (distância).

dis.bc<-function(dados)
	{
	nplot=dim(dados)[2]
	similar=matrix(NA,ncol=nplot,nrow=nplot)
	rownames(similar)<-paste("plot", c(1:nplot))
	colnames(similar)<-paste("plot", c(1:nplot))
		for(i in 1:(nplot-1))
		{
		m=i+1
			for(m in m:nplot)
			{
			bc.dist=sum(abs(dados[,i]-dados[,m]))/(sum (dados[,c(i,m)]))
			similar[m,i]=bc.dist
			}
		}
	return(round(similar,3))
	}

• 1. usar a função acima para produzir a matriz de dissimilaridade:

dis1.cont=dis.bc(com1.cont)

• 2. Calcular a soma das distâncias de cada uma das parcelas:

somadist1.cont=apply(dis1.cont, 1, sum, na.rm=TRUE)+ apply(dis1.cont,2,sum, na.rm=TRUE)
somadist1.cont

• 3. Assinalar a parcela com a maior soma de distâncias ¹⁾ e guarda o seu valor como o ínicio do primeiro eixo. Essa é nossa primeira referência no espaço de descrição das nossa parcelas (ax).

max(somadist1.cont)

nomes.parc = names(somadist1.cont)
parc.ax = nomes.parc[somadist1.cont==max(somadist1.cont)][1]
parc.ax

• 4 Encontre agora a parcela que tem a maior distância da primeira referência. Caso tenham várias, ficaremos com aquela que tem maior soma de distâncias. Essa é nossa segunda referência no nosso espaço de descrição (bx)

dis1.cont[,parc.ax]
dis1.cont[parc.ax,]
dist.ax=rbind(dis1.cont[,parc.ax], dis1.cont[parc.ax,])
dist.ax
dist.ax=apply(dist.ax,2,sum, na.rm=TRUE)
dist.ax
max.ax=max(dist.ax)
max.ax
parc.bx=nomes.parc[dist.ax==max.ax]
parc.bx

• 4a. Verificando se há mais parcela com a maior distância da parc.ax e selecionando aquela com maior soma de distâncias.

max(somadist1.cont[parc.bx])
somamax.bx=max(somadist1.cont[parc.bx])
parc.bx=parc.bx[somadist1.cont==somamax.bx][1]
parc.bx

• 5. Agora que temos duas referências do primeiro eixo (ax e bx), podemos calcular os valores para esse eixo x de todas as outras parcelas. Isso funciona como a triangulação que usada em telemetria para encontrar um animal que está usando um emissor de rádio. Colocando receptores em dois pontos conhecidos e com a informação da distância do emissor (o animal com um rádio colar por exemplo) aos dois receptores, é possível calcular as coordenadas em que o animal está. Veja a representação gráfica do que estamos dizendo:

Para o calculo utilizamos a fórmula de Beal (1965) que nada mais é do que resolver a equação da hipotenusa dos dois triangulas acima, mais ou menos nessa sequência: Para o triangulo da direita:

$$ dist_{ax_i}^2 = x_i^2 + y_i^2$$

portanto:

$$ y_i^2 = dist_{ax_i}^2 - x_i^2 $$ (1)

Para o triangulo da esquerda:

$$ dist_{ay_i}^2 = (L-x_i)^2 + y_i^2 $$

Podemos agora substituir o $$y_i^2$$ da expressão acima pela (1) e isolar o $$ x_i$$:

$$ dist_{ay_i}^2 = (L-x_i)^2 + dist_{ax_i}^2 - x_i^2 $$

$$ dist_{ay_i}^2 = L^2 - 2Lx_i + x_i^2 + dist_{ax_i}^2 - x_i^2 $$

$$ x_i^2 - x_i^2 - 2Lx_i = L^2 + dist_{ax_i}^2 - dist_{ay_i}^2 $$

Simplificando a expressão chegamos finalmente à formula de Beal:

$$ x_i \ = \ ( L^2 \ + \ dist_{ax_i}^2 \ - \ dist_{bx_i}^2 )/ (2L) $$

• 5.1.Vamos primeiro organizar os valores de distância das parcela em relação à nossas referências para o primeiro eixo: parc.ax e parc.bx. Para a parc.ax já organizamos, agora faça o mesmo para a parc.bx

dist.ax
dist.bx=rbind(dis1.cont[,parc.bx], dis1.cont[parc.bx,])
dist.bx
dist.bx=apply(dist.bx,2,sum, na.rm=TRUE)
dist.bx

• 5.2. Aplique a fórmula para encontrar o valor do eixo x:

xi= (max.ax^2 + dist.ax^2 - dist.bx^2)/(2*max.ax)
xi

• 6. Agora que tem os valores do eixo x de todas as parcelas podemos calcular o valor do segundo eixo dado pelo teorema de pitágoras:

$$ y_i = sqrt(dist_{ax_i}^2 - x_i^2) $$

yi=sqrt((dist.ax)^2-xi^2)
yi

• 6.1. Ajuste o valor da parc.bx no eixo yi:

yi[parc.bx]=max.ax
yi

• 7. Temos agora os valores do eixo x e y, vamos organizá-los em um único objeto e fazer um gráfico:

op1.cont=data.frame(xi,yi)
op1.cont
plot(op1.cont)

Agora vamos preparar uma função que faça essas operações para não termos que fazer tudo novamente passo a passo.

ordena.polar=function(dist)
{
somadist1.cont=apply(dist, 1, sum, na.rm=TRUE) + apply(dist,2,sum, na.rm=TRUE)
nomes.parc=names(somadist1.cont)
parc.ax=nomes.parc[somadist1.cont==max(somadist1.cont)][1]
dist.ax=rbind(dist[,parc.ax], dist[parc.ax,])
dist.ax=apply(dist.ax,2,sum, na.rm=TRUE)
max.ax=max(dist.ax)
parc.bx=nomes.parc[dist.ax==max.ax]
	if(length(parc.bx)>1)
	{
	  somamax.bx=max(somadist1.cont[parc.bx])
	  parc.bx=nomes.parc[somadist1.cont==somamax.bx][1]
	  parc.bx
	}
dist.bx=rbind(dist[,parc.bx], dist[parc.bx,])
dist.bx=apply(dist.bx,2,sum, na.rm=TRUE)
xi= (max.ax^2 + dist.ax^2 - dist.bx^2)/(2*max.ax)
yi=sqrt((dist.ax)^2-xi^2)
yi[parc.bx]=max(dist.ax)
op.xy=data.frame(xi,yi)
plot(op.xy, pch=19, col=rainbow(length(xi)), xlim=c(-0.1, 1), ylim=c(-0.1,1), main="Ordenação Polar", sub="Distância Bray-Curtis")
text(op.xy-0.05, labels=rownames(op.xy))
return(op.xy)
}

Vamos aplicar a função para os dados da comunidade virtual contínua e ver se nossos cálculos estão corretos.

dist1=dis.bc(com1.cont)
ordena.polar(dist1)

Agora que já temos a função, vamos aplicá-la para as suas comunidades virtuais. Em seguida interprete os padrões abservado tendo em vista a sua comunidade virtual e as características com que a construiu.

Algumas dicas de interpretação de resultados de ordenações, não só da Ordenação Polar, baseadas no material produzido por Michael Palmer em seu, visualmente não muito atraente, mas ótimo site sobre ordenação:

1. A direção dos eixos é arbitraria e não deve afetar a interpretação
2. A escala numerica do eixos não é muito útil para a interpretação (existem algumas exceções como DCA, onde a escala é em unidades de beta diversidade)
3. Na OP, assim como muitas outras técnicas de ordenação, a ordem dos eixos é importante. Assim o eixo 1 é mais importante para a interpretação dos gradientes ambientais que o segundo.
4. A experiência prévia do sistema estudado e conhecimento da literatura pertinente são as ferramentas mais poderosas para a interpretação dos gradientes subjacentes ao padrão revelado pela ordenação.
5. A interpretação de outros eixos além dos dois primeiros(quando a análise produz) é possível e a decisão de onde parar é uma questão arbitrária e dependente da quantidade e qualidade dos dados. Em algumas técnicas há estatísticas que ajudam a tomar essa decisão.
6. É desejável que os eixos não sejam correlacionadas, o que é garantido por alugmas técnicas. Dessa forma é possível interpretar os eixos como gradientes diferentes.