Este tutorial em R é fruto da necessidade de explicar rapidamente a lógica de ajuste e seleção de modelos que a equipe do LET vem aplicando com sucesso para resolver problemas analíticos muito diversos.

Além da lógica simples e atraente da abordagem da verossimilhança, nos parece muito elegante ter um único procedimento básico para analisar dados tão diversos como padrões de riqueza, distribuição espacial ou estimativas de tamanhos populacionais.

Usaremos as contagens de árvores por espécie em 50 quadrados de 1 ha na parcela pemanente de Barro Colorado responder às seguintes perguntas:

1. Qual modelo de distribuição de probabilidades melhor descreve a variação no número de espécies por quadrado?
2. Há um efeito do número de indivíduos sobre a riqueza de espécies por parcela?

Para isto precisamos do número de espécies e indivíduos por quadrado. Os dados para se conseguir isto estão no objeto BCI do pacote vegan. Baixe o pacote e carregue o conjunto de dados:

require(vegan)
data(BCI)

Este objeto e um dataframe, com especies nas colunas e quadrados nas colunas. Para contar o numero de individuos por quadrado usamos a funcao apply:

 BCI.ab <- apply(BCI,1,sum)

Para contar o numero de espécies por quadrado (linha), primeiro definimos uma função que conta os elemntos diferentes de zero em um vetor, e a aplicamos a cada linha, novamente com apply:

 riq <- function(x){sum(x>0)}
 BCI.S <- apply(BCI,1,riq)

Com isto temos um vetor com as abundâncias de cada parcela e outro com as riquezas (BCI.ab e BCI.S, respectivamente).

Idealmente os modelos devem ser escolhidos por razões teóricas. Para este exemplo vamos supor que haja duas teorias concorrentes que prevêem que a densidade de espécies segue uma distribuição normal ou a distribuição log-normal.

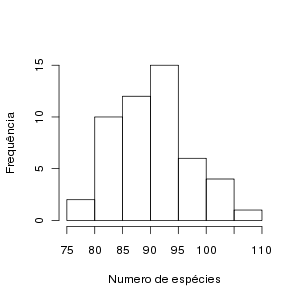
Um histograma dos dados sugere uma distribuição mais assimétrica do que a normal, indicando que a log-normal pode ser mais adequada:

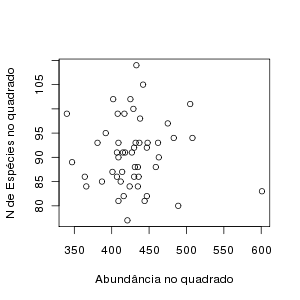
A segunda pergunta é sobre a relação entre abundância e riqueza em cada quadrado, o que podemos inspecionar com um gráfico de dispersão:

plot(BCI.S~BCI.ab, xlab="Abundância no quadrado", ylab="N de Espécies no quadrado"), que mostra uma relação que parece poder ser aproximada por uma equação de reta:

Não há um padrão muito evidente, mas podemos definir um modelo linear em que o valor esperado de riqueza em cada quadrado seja uma função linear da abundância.

Os modelos estatísticos que usamos aqui têm a forma geral:

$$ Y ~ F(y | \theta) $$

Que lemos como:

<box red>“A variável dependente $$Y$$ segue uma distribuição de probabilidades $$F$$ que tem um conjunto de parâmetros, representados por $$\theta$$”. </box>

Para cada combinação de valores de $$\theta$$, esta função atribui a cada valor observado $$y$$ uma probabilidade ou densidade de probabilidade.

Ajustar um modelo deste tipo pelo critério de máxima verossimilhança é buscar os valores dos parâmetros dos modelos que resultam no modelo mais plausível.

Se aceitamos que nossa variável de interesse $$y$$ pode ser descrita por uma função de distribuição de probabilidades (PDF) com parâmetros $$\theta$$:

$$F(y | \theta)$$

e se temos um conjunto $$Y$$ de $$N$$ valores $$y_i$$, a verossimilhança é qualquer função proporcional ao produto obtido pela PDF para cada valor de $$y$$:

$$L(\theta | Y) \prop prod_1^N\ F(y_i |\theta)$$

Mesmo com poucos valores estes produtos são números muito pequenos, mais baixos que a precisão de nossos computadores. Para resolver isto, e para transformar o produto numa soma, definimos a função de log-verossimilhança:

$$LL(\theta | Y) = c.sum_1^N\ log\ F(x_i | \theta)$$

sendo $$c$$ uma constante qualquer.

A funções de verossimilhança e log-verossimilhança expressam o valor de evidência que um conjunto de dados tem para sustentar um dado modelo, em comparação com outros concorrentes. Ela fornecem uma medida direta de plausibilidade de diferentes explicações que podemos ter para nossos dados.

O primeiro passo para o ajuste é definir a função de log-verossimilhança para cada um dos modelos. Nesta função, fixamos os dados e deixamos os parâmetros livres para variar, o que representamos por $$LL(\theta | Y)$$. Em outras palavras, a função de verossimilhança é uma função dos parâmetros, condicionada aos dados.

A constante $$c$$ da função de log-verossimilhança pode ter qualquer valor, inclusive $$1$$. Neste caso ela será a soma dos logaritmos das probabilidades que o modelo atribui a cada dado. Com isto temos uma maneira simples de definir funções de log-verossimilhança no R.

Nosso primeiro modelo é a distribuição normal, que tem os paramêtros $$\mu$$ e $$\sigma$$, que correspondem à média e desvio-padrão. Vamos definir no R uma função de log-verossimilhança, que é simplesmente a soma do log da densidade de probabilidade atribuida a cada dado por uma normal, com um certo valor de $$\mu$$ e de $$\sigma$$:

 LL.norm <- function(media,desvio) { -sum(dnorm(BCI.S, mean=media, sd=desvio, log=T)) }

• Note que os dados estão declarados dentro da função, ou seja, são fixos. Esta função serve apenas para este conjunto de dados. Para outro, seria preciso definir outra função, o que é coerente com a ideia de que a verossimilhança é condicionada aos dados.
• O o que pode variar são os argumentos da função, que são os parâmetros da normal.
• O argumento log=T faz com as probabilidades sejam transformadas para seu logaritmo.
• Multiplicamos a soma por -1 (sinal negativo na função), para que o máximo de verossimilhança torne-se um mínimo. Isso é apenas um artifício para usar rotinas computacionais de minimização (veja a seguir).

Seguindo o mesmo raciocínio, definimos a função de log-verossimilhança para a log-normal, que tem parâmetros $$\mu$$ e $$\sigma$$ (meanlog e sdlog no R, respectivamente), que são a média e o desvio-padrão dos logarítmos de $$y$$:

    LL.lnorm <- function(lmedia,ldesvio) { -sum(dlnorm(BCI.S, meanlog=media, sdlog=desvio, log=T)) }

Por fim, definimos o terceiro modelo, em que o valor esperado da riqueza por quadrado é uma função linear da abundância no quadrado. Como o valor esperado é a média de uma distribuição, a função de verossimilhança deste modelo é :

LL.norm.ab <- function(a,b,desvio) {
  media=a+b*BCI.ab
  -sum(dnorm(BCI.S, mean=media, sd=desvio, log=T)) }

• Na normal a média corresponde ao parâmetro $$\mu$$. Por isso o substituímos pela relação linear com abundância.
• Note que este modelo tem três parâmetros: o desvio-padrão $$\sigma$$, e a inclinação e intercepto da relação com abundância, que definem a média.

Um mesmo modelo pode ter diferentes verossimilhanças, de acordo com os valores de seus parâmetros. O maior valor de verossimilhança que podemos obter com um modelo é uma medida do quão plausível ele é como explicação para os dados.

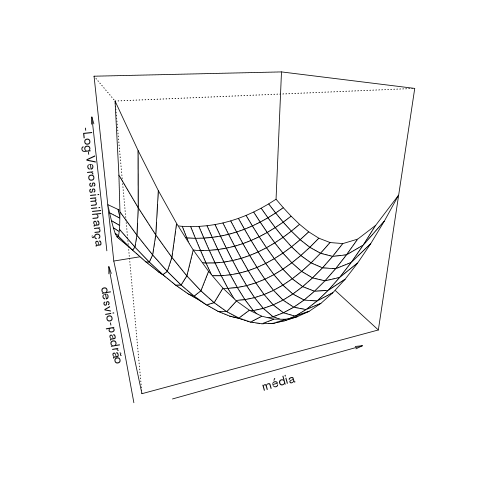
A figura abaixo mostra a superfície definida pela verossimilhança do modelo normal dos dados de BCI para diferentes valores dos parâmetros $$\mu$$ e $$\sigma$$. Como a escala está em log-verossimilhança negativa, a máxima verossimilhança equivale a um mínimo neste gráfico.

No R há algumas rotinas de otimização, que “experimentam” diferentes combinações dos parâmetros de uma função para encontrar um mínimo (ou máximo). Portanto, para encontrar o valor de máxima verossimilhança basta aplicar esta otimização às nossas funções de log-verossimilhança definidas acima.

A função mle2 do pacote bbmle é bastante eficiente para isto, mas precisa de algum valor inicial dos parâmetros, a partir dos quais ela começa a varrer o conjunto de parâmetros. Criamos três objetos para guardar os resultados das otimizações das funções de verossimilhança de cada modelo:

require(bbmle)
BCI.norm <- mle2(LL.norm, start=list(media=90, desvio=7))
BCI.lnorm <-  mle2(LL.lnorm, start=list(lmedia=4, ldesvio=0.07))
BCI.norm.ab <- mle2(LL.norm.ab, start=list(a=1, b=1, desvio=7))

Uma vez encontrado o valor de máxima verossimilhança de cada modelo podemos compará-los. Lembrando que a verossimilhança é uma medida de plausibilidade, ficamos com o modelo que tem a maior verossimilhança.

No objeto criado com a função mle2 há o valor de log-verossimilhança obtido com a otimização, que corresponde à máxima verossimilhança (ou à mínima log-verossimilhança). Podemos extraí-lo com a função logLik, do pacote /MASS/:

> require(MASS)
Carregando pacotes exigidos: MASS
> logLik(BCI.norm)
'log Lik.' -167.7746 (df=2)
> logLik(BCI.lnorm)
'log Lik.' -167.18 (df=2)
> logLik(BCI.norm.ab)
'log Lik.' -167.7689 (df=3)

Embora a log-verossimilhança do modelo log-normal seja menor que o do modelo log-normal, a diferença é muito pequena¹⁾, portanto ambos são explicações igualmente plausíveis para os dados.

O modelo com efeito da abundância sobre a riqueza tem também uma pequena diferença de log-verossimilhança, mas é menos parcimonioso. Quando os modelos têm números diferentes de parâmetros, é melhor compará-los com o AIC, que faz um compromisso entre plausibilidade e complexidade dos modelos:

> AIC(BCI.norm)
[1] 339.5492
> AIC(BCI.lnorm)
[1] 338.36
> AIC(BCI.norm.ab)
[1] 341.5378

O AIC expressa corretamente que o modelo com efeito do número de indivíduos não dá nenhum ganho de plausibilidade, embora seja mais complexo (um parâmetro a mais).

Agora que conhecemos os modelos mais simples e plausíveis, podemos inspecionar os valores estimados de seus parâmetros, que são aqueles associados à máxima verossimilhança ²⁾. Os valores estimados e seus intervalos de confiança podem ser obtidos:

> coef(BCI.norm)
    media    desvio 
90.780077  6.934819 
> coef(BCI.lnorm)
   lmedia   ldesvio 
4.5055578 0.0757169 
> confint(BCI.norm)
Profiling...
           2.5 %    97.5 %
media  88.820057 92.739943
desvio  5.770096  8.552818
> confint(BCI.lnorm)
Profiling...
             2.5 %     97.5 %
lmedia  4.48416154 4.52695426
ldesvio 0.06299136 0.09336946

E com os valores estimados podemos traçar uma curva dos valores previstos pelos modelos sobre o histograma:

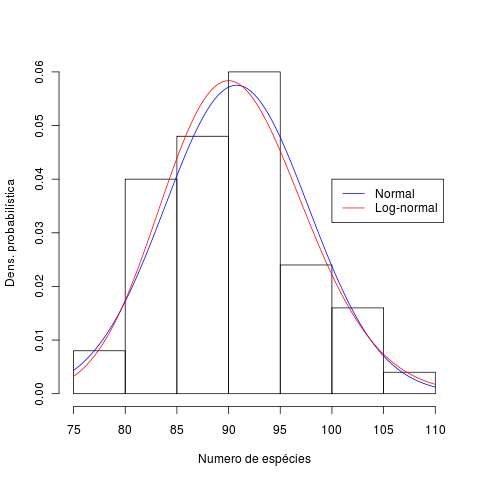
Examine os valores dos parâmetros do modelo selecionado e interprete-os biologicamente.

Por exemplo, no modelo normal, a parâmetro $$\mu$$ informa sobre a densidade média de espécies, e $$\sigma$$ sobre o quanto ela varia, ou seja, sobre alguma heterogeneidade dentro da área.