Tabela de conteúdos
Verossimilhança
 Para esse primeiro exercício utilizaremos excepcionalmente o programa Excel. Não se acostume com isso, o programa não merece sua confiança. Caso tenha conhecimento da linguagem R e queira utilizar essa MARAVILHOSA ferramenta sugerimos fortemente que tente montar um script a partir desse roteiro. Para ver um pseudo-código de de verossimilhança no R veja o roteiro Verossimilhança no R
Para esse primeiro exercício utilizaremos excepcionalmente o programa Excel. Não se acostume com isso, o programa não merece sua confiança. Caso tenha conhecimento da linguagem R e queira utilizar essa MARAVILHOSA ferramenta sugerimos fortemente que tente montar um script a partir desse roteiro. Para ver um pseudo-código de de verossimilhança no R veja o roteiro Verossimilhança no R
Uma ótima leitura introdutória para verossimilhança é o texto batista2009.pdf do Prof. João Baptista, responsável pela disciplina de Modelos estatísticos no nosso programa, junto com o Prof. Paulo Inácio.
Exercício - Máxima Verossimilhança
Este é um exercício sobre o Método da Máxima Verossimilhança, utilizando os dados de presença e ausência, muito comuns em trabalhos de levantamento de populações animais. Consiste em amostrar algumas localidades (unidades amostrais) e registrar a presença ou não de algum indivíduo da espécie. No exemplo que vamos utilizar, o pesquisador retornou a cada localidade cinco vezes, em um intervalo em que seja razoável a premissa de fechamento 1).
Objetivos:
O principal objetivo desse exercício é entender o que significa estimar parâmetros com o método de máxima verossimilhança. Para isso vamos:
a) Obter estimativa da máximo verossimilhança dos parâmetros:
- probabilidade de ocorrência: $\psi$
- probabilidade de detecção: $p$
b) Representar graficamente a superfície de verosimilhança.
1) Um conjunto de observações fictícios.
- Os dados estão em uma matriz [i,j], com número i de linhas (localidades) e j de colunas (ocasiões).
- Como tratam-se de dados de presença e ausência, vamos representar as ausências por zeros, e as presenças por um.
Exemplo: <WRAP center round box 60%>
| local | t1 | t2 | t3 | t4 | t5 | Soma |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 | 1 | 3 |
| 3 | 1 | 1 | 0 | 0 | 0 | 2 |
| 4 | 0 | 1 | 0 | 1 | 0 | 2 |
| 5 | 0 | 0 | 1 | 1 | 1 | 3 |
| 6 | 1 | 0 | 0 | 0 | 0 | 1 |
| 7 | 0 | 1 | 1 | 1 | 1 | 4 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 0 | 0 | 1 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 |
</WRAP>
2)Um um modelo simples de ocorrência com dois parâmetros, leva em conta:
- $\psi$ é a probabilidade de ocorrência, relativa aos locais (LINHAS);
- $p$ é a detecção (condicionada à ocorrência), relativa ao momento da amostragem (COLUNAS);
A somatória das linhas é o número de detecções da espécie em cada localidade.
Calculando Probabilidades
Nos locais em que a espécie não foi registrada em nenhum dos tempos, a soma das observações ($n_i=\sum_i x_{ij}$) é zero a temos duas possibilidades:
- a espécie não ocorre na localidade, ou
- a espécie ocorre na localidade e não foi detectada em nenhuma ocasião.
Podemos calcular essa probabilidade 2):
<WRAP center round box 80%> <wrap em>probabilidade de não ocorrer ou ocorrer e não ser detectada em cinco ocasiões: </wrap>
\begin{equation} \label{eq:1} P(n=0) =(1-\psi) + \psi(1-p)^5 \end{equation} </WRAP>
A primeira parte da expressão acima $(1-\psi)$ é a probabilidade de não ocorrer e a segunda parte é composta pela probabilidade de ocorrer $\psi$ vezes a probabilidade de não ser detectado em cinco ocasiões $ (1-p)^5 $.
Quando a soma das observações em uma localidade ($n_i$) é maior que zero, ou seja a espécie foi observada em pelo menos uma das ocasiões, o cálculo da probabilidade é: <WRAP center round box 60%> <wrap em>probabilidade de ocorrer e ser detectado $n$ vezes e não ser detectados nas outra amostras (total - $n_i$): </wrap>
\begin{equation} \label{eq:2} P(n) = \psi p^{n_i} (1-p)^{5-n_i} \end{equation}
</WRAP>
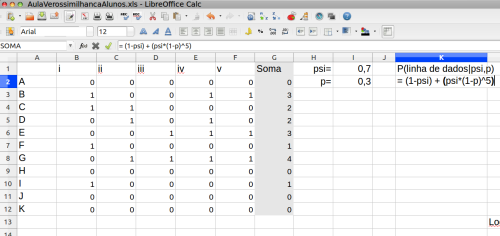
Com isso temos o equações que expressam o registro das espécie em função da sua ocorrência e detecção, que são quantidades desconhecidas. Só conhecemos $n_i$, o número de ocasiões em que a espécie foi registrada em cada localidade. Mas podemos usar as expressões \ref{eq:1} e \ref{eq:2} para calcular a probabilidade que uma certa combinação de $\psi$ e $p$ atribui a cada uma de nossas observações. Vamos fazer este cálculo para $\psi=0,7$ e $p=0,3$:
- abra a planilha do excel com os dados;
- faça a soma das ocorrências para cada localidade;
- insira as expressões acima em cada linha, dependendo se houve alguma ocorrência (equação \ref{eq:2}) ou não (equação \ref{eq:1}) da espécie na localidade;
- faça a multiplicação desses valores ao final da coluna.
</WRAP>
Muito bem! Acabamos de calcular a verossimilhança para os valores dos parâmetros $\psi=0,7$ e $p=0,30$. Imagine que existe uma probabilidade de encontrar os dados observados, dados esses parâmetros. A verossimilhança pode ser qualquer quantidade proporcional a esta probabilidade. Em linguagem matemática:
$$\mathcal{L} \ = \ k P(\text{dados}|\text{parâmetros})$$
Onde $k$ é qualquer valor constante, o que nos permite dividir ou multiplicar a verossimilhança por qualquer constante. Isso muitas vezes ajuda nos cálculos. Neste exercício não precisaremos disso, e fazemos $k=1$ e portanto a verossimilhança será o próprio valor da probabilidade dos dados obtida com cada valor dos parâmetros:
$$\mathcal{L} \ = \ P(\text{dados}|\text{parâmetros})$$
Que se lê “probabilidade atribuída aos dados, condicionada aos valores dos parâmetros”.
Função de Verossimilhança
Vamos formalizar melhor a função de verossimilhança. Ela é a função que descreve a probabilidade que diferentes valores de parâmetros atribuem aos dados observados, definida como:
<WRAP center round box 60%> <WRAP round center centeralign notice > Função de Verossimilhança </WRAP> $$\mathcal{L} (\theta | X = x)$$ </WRAP>
onde:
- $X$ é uma variável medida, descrita por um modelo probabilístico;
- $x$ representa valores obtidos numa medida ou amostra (os dados!);
- “$| X = x$” se lê “dado que $X=x$” (ou seja, que os dados têm os valores observados $x$);
- $\theta$ representa o conjunto de parâmetros que definem o modelo probabilístico.
Notem que nós invertemos os argumentos da função: os parâmetros do nosso modelo agora estão funcionando como variáveis de uma nova função, que é a verossimilhança.
Agora podemos definir uma função de verossimilhança para os dados tratados aqui. É o mesmo calculo feito acima, apenas deixando os parâmetros $\psi$ e $p$ como incógnitas.
<WRAP center round box 60%> <wrap em>Em quatro localidades não houve registros em nenhuma ocasião:</wrap> $$ \mathcal{L}_0=(1-\psi) + \psi (1-p)^5 $$ <wrap em>Em duas localidades houve registro apenas um vez:</wrap> $$ \mathcal{L}_1=(\psi p^1) (1-p)^4 $$ <wrap em>Em duas localidades houve registros duas vezes:</wrap> $$ \mathcal{L}_2=(\psi p^2) (1-p)^3 $$ <wrap em>Em duas localidades houve registro três vezes:</wrap> $$ \mathcal{L}_3=(\psi p^3) (1-p)^2 $$ <wrap em>Em uma localidade houve registro quatro vezes:</wrap> $$ \mathcal{L}_4=(\psi p^4) (1-p)^1 $$
</WRAP>
Multiplicando as verossimilhanças para cada localidade obtemos a probabilidade que os parâmetros atribuem ao conjunto de dados observados 3):
<WRAP center round box 100%> <wrap em> Verossimilhança = </wrap> $\mathcal{L}_0^4 \times \mathcal{L}_1^2 \times \mathcal{L}_2^2 \times \mathcal{L}_3^2 \times \mathcal{L}_4$
</WRAP>
Parece uma expressão complicada, mas se acompanhou passo a passo os caminhos até aqui e entendeu a ideia, é só não errar nenhum parênteses que essa fórmula funciona como nossa função de verossimilhança. Quando calculamos a verossimilhança para os valores dos parâmetro $\psi =0,7$ e $p=0,3$ encontramos um valor muito pequeno 4). Estes valores podem facilmente ficar abaixo da precisão numérica do computador. Para não correr o risco desses pequenos valores desaparecerem dos nossos cálculos, vamos utilizar uma transformação matemática que faz com que o valor muito próxima a zero tenha, em módulo, um número que é mais fácil de tratar: o logaritmo. Duas regras básicas operações de logaritmo vão nos ajudar a simplificar a expressão acima:
<WRAP center round box 60%> $$ \log(xy) = \log(x) + \log(y)$$ $$ \log(x^y) = y\log(x) $$ </WRAP>
Aplicando essas duas regras nossa expressão acima fica: <WRAP center round box 100%> <wrap em> Log-Verossimilhança = </wrap> $4 \log \mathcal{L}_0+ 2 \log \mathcal{L}_1 + 2 \log \mathcal{L}_2 + 2 \log \mathcal{L}_3 + \log \mathcal{L}_4$ </WRAP> Como logarítmos de números próximos a zero ($0<x<1$) são negativos, vamos completar nossa transformação multiplicamos o valor da Log-Verossimilhança por $-1$ para obter a Log-Verossimilhança negativa. Como a escala e o sinal do valor foram modificados por nossa transformação, agora os valores de -Log-Verossimilhança maiores indicam verossimilhanças menores e valores pequenos, verossimilhanças maiores.
Vamos calcular então o valor de -logaritmo da verossimilhança para diferentes valores de parâmetros no Excel, usando a expressão acima.
<WRAP center round box 60%>
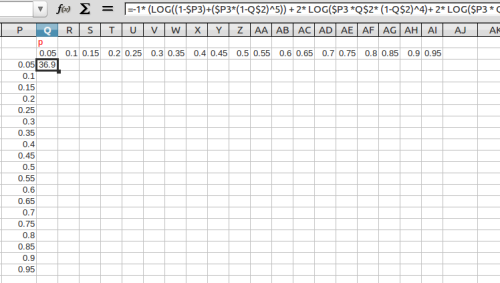
- crie uma coluna com valores de $\psi$ de 0.05 até 0.95 a cada 0.05;
- faça o mesmo para a linha para valores de $p$, formando um quadro;
- digite a fórmula da -Log-Verossimilhança usando a referência dos valores de $\psi$ e $p$;
- copie a formula para todo o quadro de valores;
</WRAP>
<WRAP center round box 60%> <WRAP round center centeralign notice > Dica </WRAP> Para manter o valor de uma célula fixa na fórmula do Excel, use o simbolo $.
- valor da célula A1 fixo: \$A\$1
- apenas a coluna fixa: $A1
- apenas a linha fixa: A$1
Quando colocar na formula o p, utilize a indexação da posição dele com \$ antes da letra da coluna (\$A1), no caso do psi faça ao contrário fixe a linha (A\$1). </WRAP>
<WRAP center round 60%>
Faça um gráfico com os valores dos parâmetros no eixo x ($p$) e y ($\psi$) e no eixo z inclua os valores de log-verossimilhança negativa. </WRAP>
Máxima Verossimilhança
Acabamos de construir a superfície de verossimilhança do nosso modelo! Poderia ter sido melhor, poderíamos ter usado intervalos muito menores de $\psi$ e $p$, se possível intervalos infinitesimalmente pequenos, o que nos daria a superfície contínua dos possíveis valores de parâmetros. Para nossa proposta aqui, intervalos de 0,05, bastam.
<WRAP center round box 60%> <WRAP round center centeralign notice > Afinal, o que queremos com isso?! </WRAP>
Queremos os valores de parâmetros que atribuem a maior probabilidade aos dados observados!
- Ou seja, nossa melhor estimativa para os parâmetros $p$ e $\psi$ são os que atribuem mais probabilidade ao que observamos, que são os dados. Se aceitamos isso, podemos dizer que essa estimativa são os valores mais plausíveis, ou mais verossímeis dos parâmetros para esse conjunto de dados.
- Como a verossimilhança nos ajuda a chegar a esses valores? Os valores mais plausíveis dos parâmetros são os aqueles para os quais a verossimilhança é máxima. Portanto, os valores que geram o menor valor de Log-Verossimilhança negativa.
</WRAP>
<WRAP center round box 60%>
 </WRAP>
</WRAP>
<WRAP center round todo 60%>
- quais o parâmetros que maximizam a verossimilhança para nossos dados?
- varie os valores dos dados (tabela com 0 e 1) e veja se sua intuição quanto ao valor de $\psi$ e $p$ dos dados hipotéticos se aproxima à estimativa LogLike.
</WRAP>